An Approach to the Characteristics of Numbers

by Frank C. Fung ( 816 pages ) - 1st published in November / 2003

( this paper is dedicated to Charles H.L. Fung 1909-2002 )

This paper looks at the multiplication of numbers .

KEY FINDINGS :

Finding #1 : The hyperbola :

• Every multiplication { Z = X * Y } has associated with it a { Difference-Of-Squares } equation : { Z = V^2 - U^2 } , with [ V ] & [ U ] being the { Half-Sum } & { Half-Difference } respectively.

  In paticular a { positive 'odd' integer } of the format '4*K + 1' can be expressed in the format :

  • { positive 'odd' integer } = { 'odd' number }^2 - { 'even' number }^2

  And a { positive 'odd' integer } of the format '4*K + 3' can be expressed in the format :

  • { positive 'odd' integer } = { 'even' number }^2 - { 'odd' number }^2

Finding #2 : Fermat 'Sum-of-Two-Squares' equation :

• Every 'C-TYPE' equation :

  { C = D^2 + E^2 = F^2 + G^2 }

  • with { 'D' , 'F' being 'even' } & { 'E' , 'G' being 'odd' }

  has associated with it a corresponding 'Q-Type' equation :

  { Q = D^2 - F^2 = G^2 - E^2 }

  • ( assume 'D' > 'F' )

• Setting { Q = [ 2^(POT-Q) ] * [ IQ-ODD ] } , where :

  • [ 2^(POT-Q) ] is an { integer-'Power-of-'2'' } and (POT-Q) is the Power-Of-Two for 'Q'

  • [ IQ-ODD ] is a { positive 'odd' integer }

  permitted us to :

  • expand the equation { Q = G^2 - E^2 } involving [ 'odd' squares ] via :

    • the [ integer grid-points ] on the hyperbola { IQ-ODD = IETA-ODD * IZETA-ODD }

  • expand the equation { Q = D^2 - F^2 } involving [ 'even' squares ] via :

    • the [ integer grid-points ] on the hyperbola { IQ-ODD = IETA-ODD * IZETA-ODD } , using a procedure similar to the one usd for [ 'odd' squares ] above, but with a new 'twist'.

    • the [ 'Difference-Of-Squares' ] ' expansion procedure in 'Findings #1' above, whenever [ POT-Q ] is 'even', in addition to the procedure immediately above.

  • The 'C-Type' equation { integer grid-points } in the 4-Diensinal Space for { D , E , F , G }

Finding #3 : Fermat Numbers

• We used the 'Augmented Binary Format' which is based on the concept of 'adding' a single [ 1 ] to a [ bundle of '1's' ] , e.g. :

  • 1 1 1 1 1 1 1 + 1 = 1 0 0 0 0 0 0 0

  so that a { bundle of '1's' } in a binary number may always be replaced by :

  • adding a [ higher-ordered Power-Of-'2' ] ( symbolized by a 'red-color ball' ), and

  • subtracting a [ lower-ordered Power-Of-'2' ] ( symbolized by a 'blue-color ball' )

  We then combined adjacent { 'red-color'/'blue-color' balls' } to complete the conversion to the 'Augmented Binary Format'.

• We then have the factorization of the 5th , 6th & 7th Fermat Numbers :

  
  
  

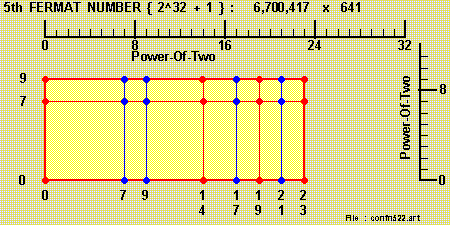
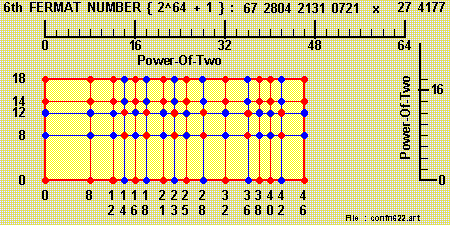
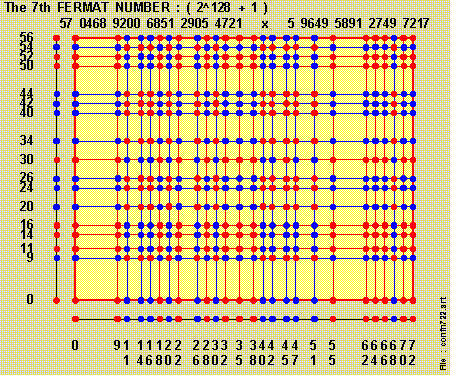
• 'Ricochet-in-the-BOX' & 'Shape-Of-BOX'

Finding #4 - The Fermat Little Theorem

• { FIRON-a/P } arises from the Fermat Little Theorem and is defiend by the value 'X' such that :

  • { a^X } = { 1 modulo P }

    • where : 'P' is 'prime' & { 0 < a <= [ P - 1 ] }

    such that:

    • { a^Y } is not equal to { 1 modulo P } for { 1 < Y < X }

• We then constructed the 'Multiplication Table' for { modulo 13 } via the 'Swing-from-the-diagonal' procedure :

  We first place 12 [ 1's ] , 12 [ 2's ] , ...... , 12 [ 12's ] on the diagonals of 12 [ 12 x 12 ] 'Square Boxes'

  

  We then 'swung-out' the numbers from the 'diagonals' to the appropriate places:

  

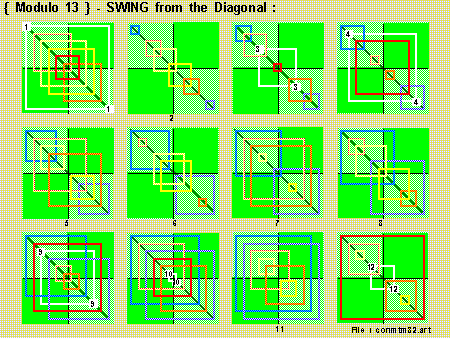
  And the numbers remaining on the 'diagonals' are marked by the 'white-color' square.

  We then combine/super-impose the 12 [ 12 x 12 ] 'Square-Box' to get our 'Multiplication Table' { modulo 13 }.

  Multiplication Tables { modulo P } can be looked at from a 'combinatorial' stand-point.

  If we used 'symbols' instead of 'numbers' on our 'Multiplication Table' for { Modulo P } and we got the 'symbols' mixed up, we would still be able to egt on with the construction, it is only a matter of selecting the 'correct' combination of 'Swing-outs-from-the diagonal' to use.

• 'Squares' on the diagonal are important and we squared the numbers remaining on the diagonal to get a reduced set of numbers

  We keep on this 'Squaring'p rocdeureto get 'redueced sets' until the size of reduced sets' no long shrinks.

  And this laid the foundation of our 'Squar-Of-Square' diagrams :

Finding #5 - Squares-Of-Squares

• 'Keep-on-squaring' staring with the number '2' means :

  • 2 x 2 = 4 ( squaring '2' once)

  • 4 x 4 = 16 ( squaring '2' twice )

  • 16 x 16 = 256 ( squaring '2' - 3 times )

    256 x 256 = 65536 ( squaring '2' - 4 times )

  • And so-on-and-so-forth.

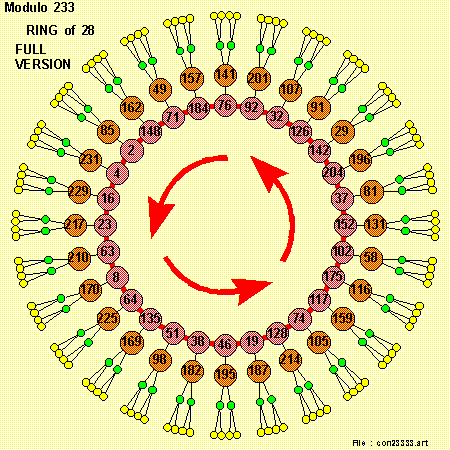
• for the 'prime' number { 233 = 8 * 29 + 1 } the equation :

  

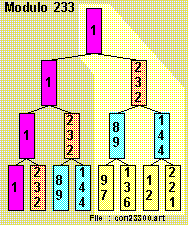
  { X^8 } = { Y modulo 233 }

  has solutions for { Y = 1 }

  and for

  { Y = 2 , 4 , 16 , 23 , 63 , 8 , 64 ,
  135 , 51 , 38 , 46 , 19 , 128 , 74 ,
  117 , 175 , 102 , 152 , 37 , 204 , 142 ,
  126 , 32 , 92 , 76 , 184 , 71, 148 }

  This latter group is then known as the 'RING-OF-28' :

  

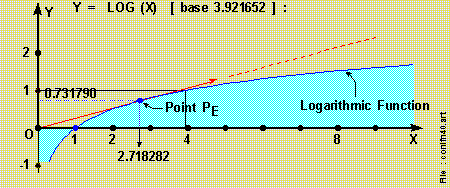
Finding #6: The Logarithmic Process

• { e = 2.718281...... } is defined via a { tangent-line } to the curve { Y = Log (X) [ base 'A' ] } passing thru the { Point-Of-Origin }, where { 1 < A < infinity }.

  And the curve may be constructed alternate via { X = A^Y }.

  

Return to FCF's HomePage