And we bring-in again the Tangent Addition Formula :
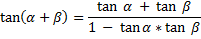
for our applications below .
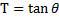
And we bring-in again the Tangent Addition Formula :
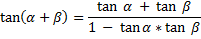
for our applications below .
to arrive at :
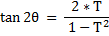
to arrive at :
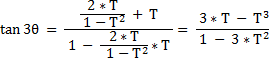
to arrive at :
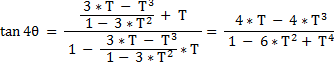
to arrive at :
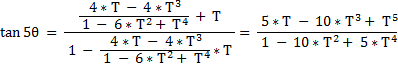
to arrive at :
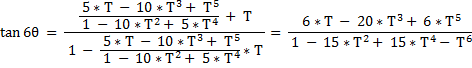
to arrive at :
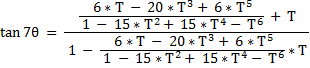
yielding :
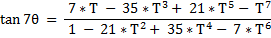
to arrive at :
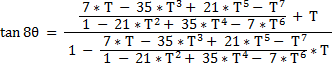
yielding :
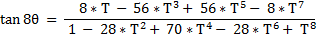
And we have :
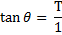
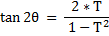
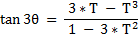
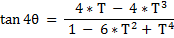
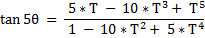
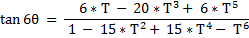
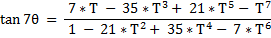
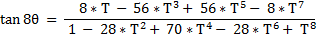
And
More details on this in the next Section coming up .