On Unique-Factorization Combinatorics via the Pascal Triangle

by Frank C. Fung ( 1st published in October, 2012. )

Top Of Page

Section XV - Summarizing on the Formulation Process

Summary for the Section :

• In this Section , we shall summarize our findings in the last 10 Sections ,
  • and give the Full Count for { Category X Composite Numbers } that can be formulated
    • with a given set of [ H ] distinct-and-different prime-numbers .

go to Top Of Page

Summarizing on { Category X Composite Numbers } :

• Let us first rephrase-and-consolidate the 10 [ QUESTIONS ] we have in the last 10 Sections ,
  • in this special format below .

  QUESTION :

  • How many distinct-and-different { Category X Composite Numbers } can we formulate
    • if we were to start-out with exactly [ Q ] prime-number/s ;

    with the 2 special conditions being that :

    • each-and-every-one of the [ Q ] prime-number/s must appear at-least-once as a prime-factor of the formulated-number [ N ] ,

      and

    • repetition of a prime-number as a prime-factor of the formulated-number [ N ] is allowed .

• We then have this table below :
  • summarizing the answers to the QUESTION's above
    • for the different values of [ Q ] .

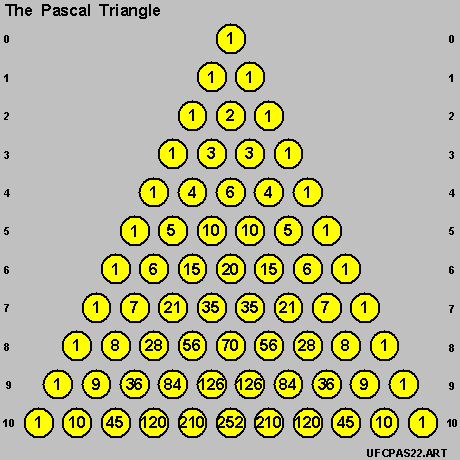
    	Value of [ Q ]
    	1	2	3	4	5	6	7	8	9	10
    **********	******	******	******	******	******	******	******	******	******	******
    Answer Quantity	1	9	36	84	126	126	84	36	9	1

  And we simply note here that :

  • the 10 values in the table above
    • are exactly the same as

    the 10 values on the [ 10th row ] of the Pascal Triangle .

  

go to Top Of Page

The Full Count for { Category X Composite Numbers } :

• Let us bring-in again this equation we established back in Section IV
  • for the Full Count of { Category X Composite Numbers } :
    • 

      

      

      

      for the case of [ H ] being greater-than-or-equal-to [ 10 ] .

  And we also present

  • this alternately format of the same equation , as follows :
    • 

      

      

      

      for the case of [ H ] being greater-than-or-equal-to [ 10 ] .

• Let us now substitute therein the values for the [ A-sub-i ]'s as established throughout the last 10 Sections ,
  • to arrive at this final equation for the Full Count :
    • 

      

      

      

      for the case of [ H ] being greater-than-or-equal-to [ 10 ] .

• And for the case of [ H ] being less-than [ 10 ] ,
  • we would simply use the 1st [ H ] terms of the above equation
    • and truncate the remaining terms ;

    to arrive at the answer to the Full Count for { Category X } .

  The reasoning for the truncation here is simply that :

  • The number of combinations for :
    • [ H ] things taken [ Q ] at-a-time is always [ zero ]
      • whenever [ Q ] is greater than [ H ] ;

    i.e :

    • 

  This then fully justifies the truncation of the terms from the above equation

  • whenever [ Q ] is greater than [ H ] .

go to Top Of Page

Confirming on the first 10 rows of the Pascal Triangle :

• It is interesting to note here that :
  • the 10 [ A-sub-i ] co-efficients associated with { Category X }

    did show up exactly-the-same as the [ 10th row ] of the Pascal Triangle .

  This prompted us to check :

  • Whether each of 9 categories from [ Category I ] thru [ Catgory IX ]
    • would have the associated { [ A-sub-i ] co-efficients }

      duplicating the corresponding row of the Pascal Triangle .

  And we were able to confirm that this is so ,

  • using a numerical evaluation procedure

    similar to the numerical procedure as outlined in the last 11 Sections .

go to Top Of Page

go to the next section : Section XVI - The formal Combinatorics Equation for { Category [ T ] }

go to the last section : Section XIV - Formulating [ Category X Numbers ] with 10 prime-numbers

return to the Unique-Factorization Combinatorics HomePage

Original dated 2012-10-08