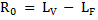Equation for the Ellipse - ( I )

An Approach to Mathematic Functions Basics

Section XIX - Equation for the Ellipse - Part I

In this Section , we shall derive the equation for the Ellipse ,
- using [ Focal Point #1 ] as the base-point for our [ Polar Co-ordinate System ] .

We shall now mark-off the distance between [ Point F1 ] and the [ Vertex 1 ] as the distance [ R-sub-zero ] ,
- i.e. :
  - with [ R-sub-zero ] having a non-zero positive value , i.e. :
  as per the diagram on-the-right above .
And we can see from this diagram that :
Consequently , we have the relation :
Let us recall , at this point , that we have already established this relation for the value of [ S ] :
- towards the end of the last Section , Section XVIII .
Thus , we can now re-express [ S ] in terms of [ R-sub-zero ] in this manner :
- based on the expression we have for [ L-sub-V ] immediately above .
And with this expression in-hand , we are now ready to proceed with the derivation process ,
- to follow immediately below .

Let us now bring-in this set of 2 diagrams below :

And we see here that , for the point [ Point P ] on the Ellipse :
And for the right-angle-triangle [ Triangle F2-Q-P ] in the diagram on-the-right above , we have :
Then , for the original [ Constant-Sum Equation ] for the ellipse , i.e. this equation :
we can now write :
And on re-arranging terms , we have :
Let us now square both sides of the equation to arrive at this :
And on further expansion on the right-hand-side , we have :
- yielding :
And on cancelling terms , we have :
Further re-arrangements then yield us this equation :
- yielding :
Let us now take a closer look at the terms within the 3 brackets in the above equation , and :
- we bring-in , from above , this expression for [ S ] in terms of [ L-sub-V ] and [ R-sub-zero ] :
Let us now substitute this into each of the 3 brackets , and :
- For the terms in the 1st bracket , we now have :
- For the terms in the 2nd bracket , we now have :
- For the terms in the 3rd bracket , we now have :
Thus , we can now re-write the original equation above in this manner :
And on re-arranging terms , we have :
- yielding :
Let us now re-write the above the above equation in this special format :
Therefore :
- yielding :

Let us now introduce the value [ Lamda ] such that :
We can then write the expression above in this easier-to-read format :
And we can now express [ R ] in terms of [ R-sub-zero ] via this equation below :
Let us recall , at the point , that the only restriction we have placed on the value of [ R-sub-zero ] is that :
- [ R-sub-zero ] must be greater than [ zero ] .
Therefore , the range for [ R-sub-zero ] is then :
And since the value of [ Lamda ] is defined as :
the range for [ Lamda ] here is then :
And the final equation we have for the Ellipse here is then :
And this is an important equation that we shall be coming back to ,
- when we look at the { linkage system for the Circle / Ellipse / Parabola / Hyperbola } ,
  - later in Section XXIII of this paper .