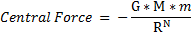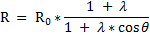An Approach to Mathematic Functions Basics

by Frank C. Fung ( 1st published in December, 2014. )

Top Of Page

go to Table Of Content below

SUMMARY and KEY FINDINGS :

Summary :

• This paper was originally intended as an in-depth study of several Mathematic Functions ,
  • in preparation of a full attack on the Riemann Zeta Function .

  But we veered off-course and found something interesting :

  • In Part VI of the papar , we looked at the Orbit of a Satellite moving under a Central Force ,
    • 

    And we threw around the idea that :

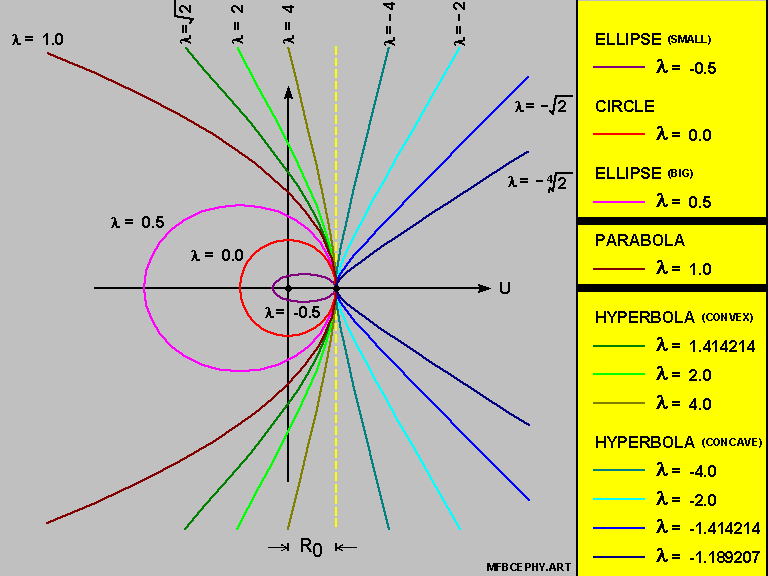
    • The Circle-Ellipse-Parabola-Hyperbola combination
      • is nothing more than a { Planar Cross-Section Cut } of 3-Dimensional Curves
        • for the value of [ N ] being equal to [ 2 ] ;

      and

      • there are other { Planar Cross-Section Cuts } for [ N = 3 ] , [ N = 4 ] , etc. .

        ( see Key Finding 2 below for more details )

Key Finding One :

• The Circle , Ellipse , Parabola , Hyperbola combination can be covered via a single type of equation of the format :
  • 

    in Polar Co-ordinates .

  

Key Finding Two :

• We looked at the orbit of a Satellite moving under a Central Force :
  • 

  We do observe that :

  • the Circular Orbit is always a possibility for { all values of [ N ] greater than [ zero ] } ;

  • and when the Mass-at-the-Center disappears , the Satellite shoots-off in a straight-line .

  The Circular Orbit and the Straight-Line Orbit are therefore anchoring orbital-shapes for { all values of [ N ] greater than [ zero ] } .

  As such ,

  • this opens up the possibility of standardization and therefore a linkage system of orbital-shapes
    • throughout the entire range for [ N ] .

Table of Content

go to Top Of Page

go to the 1st section : Section I - Introduction

return to FCF's HomePage

Original dated 2014-12-07