An Approach to Mathematic Functions Basics

by Frank C. Fung ( 1st published in December, 2014. )

Top Of Page

Section X - The Geometric Definition of the Hyperbola

Summary for the Section :

• In this Section , we shall spell-out the Geometric Definition for the Hyperbola .

go to Top Of Page

The Geometric Definition of the Hyperbola :

• We shall now do the formal Geometric Definition for the Hyperbola , as follows :

  STEP ONE :

  • We choose any two (2) points , distinct-and-separate from one-another , on a 2-dimensional plane :
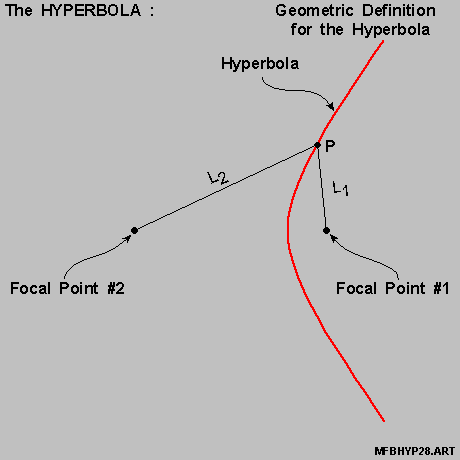
    • to serve as the 2 [ focal points ] for the Hyperbola ,
      • as marked-off as [ Focal Point #1 ] and [ Focal Point #2 ] in the diagram on-the-left below .

  

  STEP TWO :

  • We then define the loci of the Hyperbola via the following criterion :
    • IF :
      • any point [ Point P ] is a point on the Hyperbola ,

      THEN :

      • the difference between :
        • the distance from [ Point P ] to [ Focal Point #2 ]

          and

        • the distance from [ Point P ] to [ Focal Point #1 ]

        is a pre-determined constant .

      And this [ pre-determined constant ] shall remain constant-and-unchanging throughout

      • for all points on the Hyperbola .

    Furthermore ,

    • there is a special-and-specific limitation on this [ pre-determined constant ] , namely that :
      • the size of the [ pre-determined constant ] shall be less than { the distance between the 2 [ focal points ] } ,

        and

      • the size of the [ pre-determined constant ] shall be greater than or equal to [ zero ] .

• We then have this sample Hyperbola , constructed via the above-said Geometric Definition ,
  • as marked-off as the { the red-color curve } in the diagram on-the-right , above .

go to Top Of Page

Setting up the Hyperbola for our further analysis :

• We shall now set up the general Hyperbola for our further analysis in the next 4 Sections ,
  • and we shall also set up at-the-same-time the { U-V Axis System }
    • to serve as our primary [ 2 orthogonal-axis system ] for referencing .

  FIRST STEP :

  • We randomly choose any 2 points , distinct-and-separate from one-another , in a 2-dimensional plane ,
    • to serve as our [ Focal Point #1 ] and [ Focal Point #2 ] respectively ;
      • as per the diagram on-the-left below .

    We can then pass a straight-line thru the above-said 2 [ focal points ] ,

    • in the [ Focal Point #2 ] to [ Focal Point #1 ] direction ;

    and :

    • this line shall then serve as the [ U-Axis ] of our [ U-V Axis System ] .

  

  SECOND STEP :

  • We can then identify :
    • the mid-point of the { segment from [ Focal Point #2 ] to [ Focal Point #1 ] } as the point [ Point O ] ,
      • as per the diagram on-the-right above .

    We can then construct a straight-line perpendicular to the [ U-Axis ] passing thru [ Point O ] ,

    • and this line shall then serve as the [ V-Axis ] of our [ U-V Axis System ] .

  • And since [ Point O ] is the mid-point of the { segment connecting [ Focal Point #2 ] and [ Focal Point #1 ] } ,
    • [ Point O ] is in fact equi-distant from the 2 [ focal points ] .

    As such , we can now mark-off the distance from [ Point O ] to either of the [ focal points ]

    • as the distance [ L-sub-F ] , as shown in the diagram on-the-right above ;

      i.e. :

      • 

        

    And the distance between the 2 [ focal points ] is then given by :

    • 

  THIRD STEP :

  • Let us now introduce the [ pre-determined difference ] , denoted as [ D ] , such that :
    • 

    We can then construct the general Hyperbola ,

    • in accordance to the afore-said Geometric Definition as detailed above ;
      • as per the diagram on-the-left below .

  • Then , for any point [ Point P ] on the Hyperbola , we can now set up :
    • 

    • 

    And this relation :

    • 

      shall remain valid throughout for all points of the Hyperbola .

  

  FOURTH STEP :

  • Let us now identify the [ Vertex ] of the Hyperbola
    • as the point-of-intersection between the Hyperbola itself and the [ U-Axis ] ;
      • as per the diagram on-the-right above .

    We then denote the distance between [ Point O ] and the [ Vertex ] as the distance [ RHO-sub-zero ] ,

    • i.e. :
      • 

    Thus , for the [ Vertex ] :

    • the distance from the [ Vertex ] to [ Focal Point #1 ] is :
      • 

    • the distance from the [ Vertex ] to [ Focal Point #2 ] is :
      • 

    Consequently ,

    • [ D ] may now be expressed in terms of [ RHO-sub-zero ] via the following :
      • First , we bring-in again the general expression for [ D ] , i.e. :
        • 

        Substituting therein the values for [ L2 ] and [ L1 ] at the [ Vertex ] , respectively , then gives us this equation :

        • 

      • And the final expression for [ D ] here is then :
        • 

go to Top Of Page

A Special Comment here on [ RHO-sub-zero ] :

• In our Geometric Definition of the Hyperbola above ,
  • we did place a special-and-specific condition on the value of [ D ] ,

    namely that :

    • 

  Now that we have established this relation between [ D ] and [ RHO-sub-zero ] :

  • i.e. :
    • 

    it then follows that :

    • 

  Consequently ,

  • we have this restirction on the value of [ RHO-sub-zero ] :
    • 

• And that-is-to-say :
  • [ RHO-sub-zero ] is always less than [ L-sub-F ] ,

    but

    [ RHO-sub-zero ] is never equal to [ L-sub-F ] .

go to Top Of Page

What's Next :

• In the next 4 Sections to follow , we shall be deriving the equations for the Hyperbola
  • using 4 different [ co-ordinate systems ] , namely :
    • the [ U-V Axis Co-ordinate System ] with [ Point O ] as the base point-of-reference ,

    • the [ Polar Co-ordinate System ] with [ Point O ] as the base point-of-reference ,

    • the 1st [ Focal-Point based Co-ordinate System ] with [ Focal-Point #1 ] as the base point-of-reference , and

    • the 2nd [ Focal-Point based Co-ordinate System ] with [ Focal-Point #2 ] as the base point-of-reference .

  And we shall be consolidating our findings on the Hyperbola in the Section thereafter on the Asymtotes ,

  • before moving-on to Part IV on the Ellipses , the Circle , and the Parabola .

• And we shall establish , towards the end of Part IV , that :
  • the Hyperbola , the Ellipses , the Circle and the Parabola can all be expressed via a single type of equation ,

    i.e. , an equation of the format :

    • 

  And in Part V of this paper ,

  • we shall formalize the linkage system for the hyperbola / ellipse / circle / parabola ,
    • via our study of the orbit of a satellite moving under a [ central force ] .

• Lots of work ahead , so let's move on !

go to Top Of Page

go to the next section : Section XI - Equation of the Hyperbola in [ U-V Co-ordinates ]

go to the last section : Section IX - The Hyperbola in Cartesian Co-ordinates

return to the MATH Functions Basics HomePage

Original dated 2014-12-07