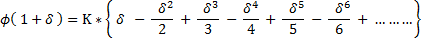
where :
- the [ PHI-of-(x) ] is any function that qualifies as a Logarithmic Function .
Consequently , the Expansion Formula for Natural Logarithms based on the above is then :
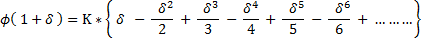
where :
Consequently , the Expansion Formula for Natural Logarithms based on the above is then :

and
We then have :

Therefore :

And we set up :
where [ n ] is any [ positive integer ] .
Let us now bring back the original Expansion Formula for Nature Logarithms from above ,

and

We can then write :

Further munipulations then yield us this relation :


And we take note at this point that :

Consequently :


Applying this to the equation immediately above then yields us this relation :


And consequently :

Thus , we can now re-write the equation above in this special format :


And the author's prefered format for the same is :

We take note here that :
we do have these rather famous results below for the Zeta Sums :

and



And we can also confirm that the Zeta Sums do converge for s = 3, 5 , 7 , etc.

And we see here that :
And this is something that we should be keeping in mind ,

involving [ complex values ] for [ s ] .