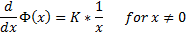- this particular relation :
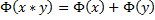
is always satisfied .
And this then is the [ Governing Relation ] defining the Logarithmic Class of Functions .
And we shall start-off the derivation process with :
whereby :
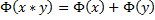
is always satisfied .
And this then is the [ Governing Relation ] defining the Logarithmic Class of Functions .
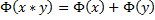
Let us now substitute the value of [ x = 1 ] into the above equation , and we have :
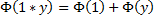
yielding :

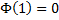
And this then is the [ First-and-Most-Important Property ] for the function [ PHI-of-(x) ] ,
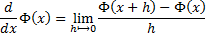
And via a simple manipulation on the right-hand-side , we do come up with this alternate format for the same equation :
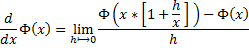
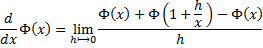
And on cancelling terms , we have :
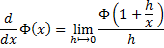
Let us now re-write the above equation in this format below for our further manipulations :
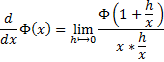
yielding :
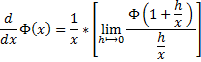
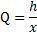
We can then write :
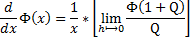
And we take note , at this point , that for [ x ] being [ not-equal-to-zero ] :
and that-is-to-say :
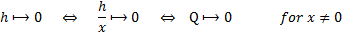
Thus , we can now re-write the above equation for the [ first-derivative of PHI ] in this manner :
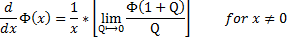
And we bring-in , at this point , the first-derivative of the [ PHI-of-(x) ] evaluated at [ x = 1 ] , defined via :
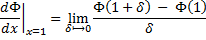
Let us again recall , from above , the [ First-and-Most-Important Property ] for the [ PHI-of-(x) ] ,
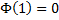
And on substituting this into the equation immediately preceding , we have this :

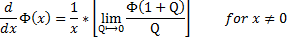
for a quick comparison .
And we see here that :
Thus , we can now express the [ first-derivative of PHI ] in the following manner :
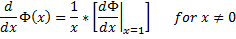
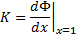
Two things to take special note of here :
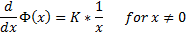
And on doing so , we have :
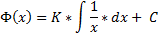
And again we recall , from above , the First-and-Most-Important Property for the [ PHI-of-(x) ] ,
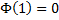
And what this tell us here then is that :
Consequently , we can now write the equation for the [ PHI-of-(x) ] in this general format :
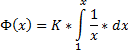
Or alternately , we can write the same equation in this special-and-specific format below :
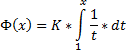
for slightly better clarity .
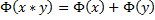
Let us now substitute therein the values [ x = z ] and [ y = 1/z ] , where :
And on doing so , we have :
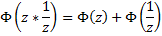
yielding :
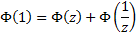
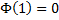
Applying this therein to the left-hand-side of the equation immediately preceding then yields us this :
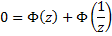
Consequently :
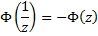
and
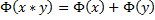
THEN :
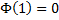
and
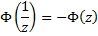
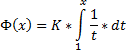
where :
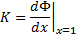
and the [ first-derivative of PHI ] is given by :