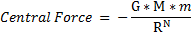An Approach to Mathematic Functions Basics

by Frank C. Fung ( 1st published in December, 2014. )

Top Of Page

Section XXXVIII - Some Observations on the Orbit of a Satellite

Summary for the Section :

• In this Section , we shall make several observations on the Orbits of the Satellite ,
  • in preparation of our { Proposal for Further Analysis } in the next Section .

go to Top Of Page

Bringing in the Kinetic Energy and the Potential Energy :

• In general , for a object of mass [ m ] moving at the velocity [ V ] ,
  • the Kinetic Energy is given by :
    • 

  And for a Satellite moving under the influence of a Central Force ,

  • the Potential Energy is given by :
    • 

  Consequently , for a Gravitation-Type Central Force varying as the { inverse of [ R-raised-to-the-Nth-power ] } ,

  • i.e. :
    • 

    the Potential Energy is given by :

    • 

go to Top Of Page

Potential Energy for various values of [ N ] :

• The Gravitation-Type Central Force that we will be investigating here are always of-the-format :
  • 

    where [ N ] is any finite value greater than [ zero ] .

  And , in preparation for our { Proposal for Further Analysis } in the next Section ,

  • it would be appropriate for us to divide the range for [ N ] into 3 segments :
    • the First Segment for { [ N ] greater than [ 1 ] } ,

    • the Second Segment for { [ N ] equal to [ 1 ] } , and

    • the Third Seqment for { [ N ] less than [ 1 ] } ;

    based on Potential Energy considerations .

• Let us now take a look at each of these 3 Segments separately :
  • For the First Segment where { [ N ] is greater than [ 1 ] } :
    • the original Potential Energy Equation above , i.e. :
      • 

      would become :

      • 

      yielding :

      • 

      And we take note here that :

      • the Potential Energy is [ zero ] at [ R = infinity ] , and

      • the Potential Energy attains a [ finite negative value ] at [ finite values of R ] .

  • For the Second Segment where { [ N ] is equal to [ 1 ] } :
    • the original Potential Energy Equation above , i.e. :
      • 

      would become :

      • 

      yielding :

      • 

      and finally :

      • 

    • And what this Equation tells us here is that :
      • when [ N = 1 ] , there is no escape for the Satellite .

      This is because :

      • the Potenetial Energy is always [ infinit ] at any given position where [ R ] is finite ;
        • as confirmed by the equation immediately above .

      Therefore :

      • any Satellite possessing only finite Kinetic Energy
        • can never overcome the Potential Energy at that same position

          in order to escape .

  • For the Third Segment where { [ N ] is less than [ 1 ] } :
    • the original Potential Energy Equation above , i.e. :
      • 

        will need to be evaluated via numerical methods .

      But ,

      • it is most unlikely that the Satellite can escape here either .

go to Top Of Page

The Circular Orbit at [ N = 3 ] :

• Let us now take a quick look at the Circular Orbit for [ N = 3 ] ,
  • and the Central Force here is :
    • 

    

• FIRST ,
  • Let us establish the relation for [ M ] , [ R-sub-zero ] , and [ V-sub-zero ] for the Circular Orbit .

    Equating the Centripetal Force and the Central Force then yields us this relation :

    • 

    Consequently , we have this relation :

    • 

      for the Circular Orbit for [ N = 3 ] .

• SECOND ,
  • Let us establish the Potential Energy at [ R = R-sub-zero ] .

    The general equation for Potential Energy for [ N > 1 ] is :

    • 

    and for [ N = 3 ] , this then becomes :

    • 

    Let us now re-write the above equation in this format :

    • 

      for our comparison purpose immediately below .

• THIRD ,
  • Let us also establish the Kinetic Energy for the Circular Orbit .

    And the Kinetic Energy here is simply :

    • 

    Let us recall that we have establish this relation in { FIRST } above :

    • 

      for the Circular Orbit .

    Thus , we can now re-write the equation above as :

    • 

• Let us now bring in both the Kinetic Energy and the Potential Energy for the Circular Orbit for [ N = 3 ] :
  • 

  • 

    and we see here that the two are equal in absolute magnitude .

  And what this means is that :

  • the Circular Orbit for [ N = 3 ] is unstable :
    • Any slightest increase in [ V-sub-zero ] or the slightest decrease in mass [ M ]
      • would result in the Satellite escaping towards [ infinity ] .

go to Top Of Page

go to the next section : Section XXXIX - A Proposal for Further Study of Orbital Shapes

go to the last section : Section XXXVII - A Graphic Look at the Solutions for [ N = 3 ]

return to the MATH Functions Basics HomePage

Original dated 2014-12-07