For any { positive 'odd' integer } :
the associated { binary code } of [ 1's ] & [ 0's ] can be readily converted to :
- an { Odd-On-Odd Format } of [ red-color-balls ] & [ blue-color-balls ] ,
so that :
- the value of the { positive integer } may be evaluated via an expansion of the { Odd-On-Odd Equation } .
This then pave-the-way for an alternate interpretation to any { binary code } .
A quick example here , for the number [ 93 ] :
- take the { binary format } for [ 93 ] , at 7-digits :
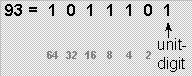
- take the { 6-digits } to-the-left of the [ unit-digit ] to form the { red-color / blue-color code } , as follows :
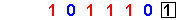
- covert these into a { red-color-ball / blue-color-ball code } , and this is the { Odd-On-Odd Format } :

- bring-in the general { Odd-On-Odd Equation } for a [ 6 color-balls code ] , as follows :
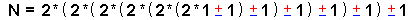
- apply the [ 6 color-balls code ] to it to arrive at :
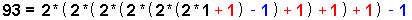
- ( a [ +1 ] for a { red-color ball } & a [ -1 ] for a { blue-color ball } . )
The key features here are :
- the expression inside of any pair of brackets always evaluates to a { positive 'odd' integer } ,
- and hence the name { Odd-On-Odd } .
- the number [ 3 ] is always involved and [ 3 ] is therefore the 'root' of all expansions .
We have , therefore , found an alternate method for expanding the { 7-digits binary code } .
The question here is :
Is a [ binary code ] always necessarily 'binary' ?
And the answer is 'NO' .
Divisibility by [ 3 ] :
We also investigated { Divisibility by [ 3 ] } using :
- the { Base-10 Format } ,
- the { Binary Format } , &
- the { Odd-On-Odd Format } .
While we did move from-left-to-right on a { Binary Code } for the { Odd-On-Odd Format } ,
- our findings here tend to indicate that a tremendous savings may be achieved here ,
when we try to determine if a { number } is divisible by a particular { prime number } .
This can be an important issue in { factorization } !