The { Odd-On-Odd Format } for { 'odd' numbers }

The { Odd-On-Odd Format } for { positive 'odd' integers } is based on the fact that :

• a { [ 4*K + 2 ] number } is always situated in-between a { [ 4*K + 3 ] number } and a { [ 4*K + 1 ] number } , so that :
  • the { [ 4*K + 3 ] number } may be expressed as :
    • ( the { [ 4*K + 2 ] number } ) + 1 ,

  • the { [ 4*K + 1 ] number } may be expressed as :
    • ( the { [ 4*K + 2 ] number } ) - 1 .

• the { [ 4*K + 2 ] number } may then be expressed as ( 2 x { a [ 2*K + 1 ] number } ) , and :
  • the { [ 2*K + 1 ] number } is always an { 'odd' number } which may be further broken-down in the same manner , as above .

• eventually , the 'odd' number [ 3 ] is reached and we can apply the 1st of two (2) { anchoring equations } , i.e. the equations :
  • 3 = 2 * 1 + 1 , &
  • 1 = 2 * 1 - 1 ;

  to complete the process .

  ( The purpose of the { 2nd anchoring equation } is explained in { Topic #3 } below . )

Let us now look at a quick example , for the number [ 67 ] , as follows :

• 67 = 2 * 33 + 1
• 33 = 2 * 17 - 1
• 17 = 2 * 9 - 1
• 9 = 2 * 5 - 1
• 5 = 2 * 3 - 1
• 3 = 2 * 1 + 1 , ( 1st anchoring equation )

We can then write :

• 67 = 2 * ( 2 * ( 2 * ( 2 * ( 2 * ( 2 * 1 + 1 ) - 1 ) - 1 ) - 1 ) - 1 ) + 1

  and this equation , featuring only [ 2's ] & [ 1's ] , is then known as the { Odd-On-Odd Equation } .

We then identify :

• each occurance of a { + 1 } with a [ red-color ball ] , and
• each occurance of a { - 1 } with a [ blue-color ball ] ,

  so that the { Odd-On-Odd Format } for the number [ 67 ] is then :

  • 

Let us now take a quick look at the { Odd-On-Odd Equation } & the { Odd-On-Odd Format } for { 'odd' numbers < 64 } , as per this table below :

Value of N	The { Odd-On-Odd Equation }	{ Odd-On-Odd } Format	Binary Format
63
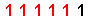
61
59
57
55
53
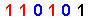
51
49
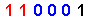
47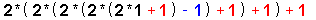
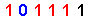
45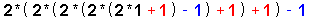
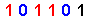
43
41
39
37
35
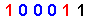
33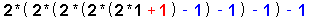
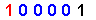
31
29
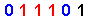
27
25
23
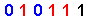
21
19
17
15
13
11
9
7
5
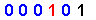
3
1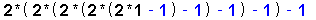

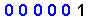
Let us take note , first-of-all , that we have marked-off , for the { Odd-On-Odd Format } ,

• the [ 1st occurance ] of a { red-color ball } with a { green-color square } ,

  when reading-off the { Odd-On-Odd Format } from left-to-right , in the usual manner .

This then mark-off the place where the value of the expression { jumps from [ 1 ] to [ 3 ] } ,

• when we evaluate the { Odd-On-Odd Equation } , expanding on a { bracket-to-bracket } basis .

Secondly , for { N = 1 } , we have repeatedly applied the { 2nd anchoring equation } , i.e. the equation :

• 1 = 2 * 1 - 1 ,

  to come with with five (5) { blue-color balls } for the { Odd-On-Odd Format } here .

This then illustrate the importance of this { 2nd anchoring equation } :

• when we repeatedly apply the { 2nd achoring equation } to the [ LEFT ] of the { 1st Occurance of a [ red-color ball ] } ,

  this process will not , and does not , alter the value of [ N ] .

And this is comparable to adding { a bunch of [ 0's ] } to the [ LEFT ] of the { 1st occurance of a [ 1 ] } in a { binary format } , reading left-to-right :

• here too , adding the said [ 0's ] will not , and does not , alter the value of [ N ] .

The reader will also notice that , for any given value of [ N ] :

• the { red-color-ball / blue-color-ball pattern } for the { Odd-On-Odd Format } , and

• the { [ 1's ] / [ 0's ] pattern } for the { binary-digits to-the-left of the [ unit-digit ] } for the { Binary Format } ,

  are always the same .

  ( And we have colored the [ 1's ] in red-color & the [ 0's ] in blue-color for the { Binary Format } in the above table for easier recognition . )

We shall explain why this is so in the next { Topic } below .

Let us now divide the { positive 'odd' integers } into layers , such that :

• { 'odd' numbers } in each layer satisfy the condition :
  • 

We then have this table below for the 1st six (6) layers :

And the { Anchoring Number } for each layer , on the very-right column , is given by :

We then have this table below for the four (4) [ anchoring numbers ] for { Layer 2 thru 5 } , for illustration purposes :

Value of N	The { Odd-On-Odd } Equation	{ Odd-On-Odd } Format	Binary Format
5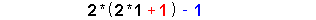
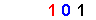
9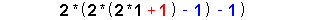
17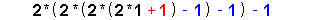
33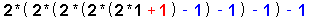

Let us now take a look at the expansion of the four (4) [ anchoring numbers ] :

This then shows why the { Odd-On-Odd Format } always matches the { Binary Code for the digits to-the-left of the [ unit-digit ] } , for these & other { Anchoring Numbers } :

• because the terms as { underlined by the green-color-line } always adds-up to [ 1 ] .

Let us start-off again with an [ anchoring number ] and change a [ blue-color-ball ] to a [ red-color-ball ] :

• this process then changes a [ -1 ] to a [ +1 ] in the { Odd-On-Odd Equation } ,
  • thereby adding a value equal to [ 2 x { an integer-power-of-[ 2 ] } ] to the value of [ N ] ;

• and this adding of the value [ 2 x { an integer-power-of-[ 2 ] } ] to the value of [ N ] will then result :
  • in a change of a [ 0 ] to a [ 1 ] in the { Binary Format } , corresponding to the added-value ;

  so that :

  • the { Odd-On-Odd Format } and the { Binary Code for digits to-the-left of the [ unit-digit ] } will always correspond .

Our interpretation here is this :

• a { Binary Code } does not necessarily have-to-be read as a 'binary' ,

  the { Odd-On-Odd Format } , and the { Odd-On-Odd Equation } arising therefrom , represents a viable alternative .