Structure of the Multiplication Table for [ modulo P ]

by Frank Charles Fung ( 1st published in June , 2006 )

Top Of Page

Epilog II : The Fractions Equation

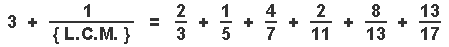
My daughter recently took an undergraduate course in { Abstract Algebra } ,

Here is a quick explanation .

First , we bring back the { Characteristic Equation } for the { Prime Numbers } 3 , 5 , 7 , 11 , 13 & 17 .

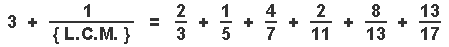
And we note that this equation is of the format :

And the { Base Solution } to this type of equations is always :

Let us now multiply the { Characteristic Equation } by [ 2 ] , to yield :

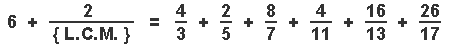
Expanding terms , we have :

Thereupon yielding the equation :

Let us now multiply the { Characteristic Equation } by [ 3 ] , to yield :

Expanding terms , we have :

Thereupon yielding the equation :

Thus , every value of { [ Z ] modulo 225,255 } , is always expressible by a unique { 6-digits code } :

Value
of
Z		 Value
of
A		 Value
of
B		 Value
of
C		 Value
of
D		 Value
of
E		 Value
of
F
0 0 0 0 0 0 0
1 2 1 4 2 8 13
2 1 2 1 4 3 9
3 0 3 5 6 11 5

And all [ codes ] are expandable via the { Characteristics Equation } :

We have therefore set-up a { coding system } for { modulo [ L.C.M. ] } .

go to Top Of Page

go to Appendix A --- Prime Numbers less than 256

go to the last section : Epilog I --- Question on Mersenne Prime

return to the HomePage for { Structure of the Multiplication Table for [ Modulo P ] }

Original dated 2006-12-31