- and for the { prime number } [ 173 = 4 x 43 + 1 ] , we bring-in :
- the { Characteristic Pyramid } , &
- the 3 x { RING's OF 14 } .
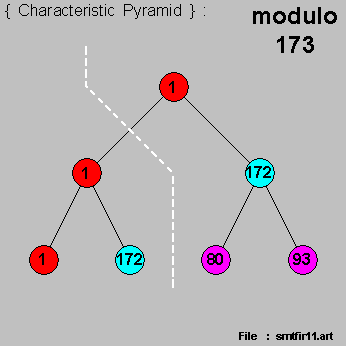
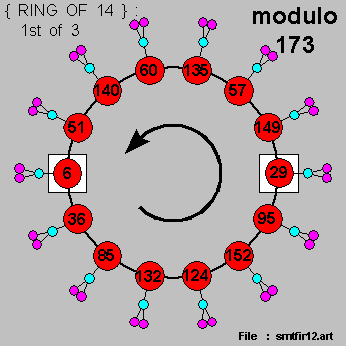


- and the { multiplicative conjugates pairs } can be readily identified , as shown above .
| Section Zero | KEY FINDINGS |
| Section I | Introduction |
| Section II | { Square-Of-Square } revisited |
| Section III | { Pyramids } & { RINGS } |
| Section IV | { Modulo 1103 } |
| Section V | { Modulo 3361 } |
| Section VI | On { FIRON-2/P } |
| Section VII | The { Chinese Remainder Theorem } revisited |
| Section VIII | Concluding Remarks |
| Appendix A | Prime Numbers less than 256 |
| Epliog I | Question on Mersenne Prime |
| Epliog II | The Fractions Equation |



