An Approach to the Triangle

In this Section , we shall be looking at Triangles in general .

In particular , we shall identify special { points } associated with the { Triangle } , and briefly describe their properties .

This then lays the foundation framework for { Section IV } , when move-on to the { Congruent-Triangles Tetrahedron } .

In general , we can identify three (3) types of { triangles } :

• the { Equilateral Triangle } :
  • where the lengths of the 3 sides are equal .

• the { Isosceles Triangle } :
  • where the lengths of 2 sides are the same and the 3rd side is of a different length .

• the { Unequal-sides Triangle } :
  • where the lengths of the 3 sides are all different .

Let us first set up , in general , a triangle --- { Triangle A-B-C } :

• with { L1 } , { L2 } & { L3 } being the lengths of the 3 sides .

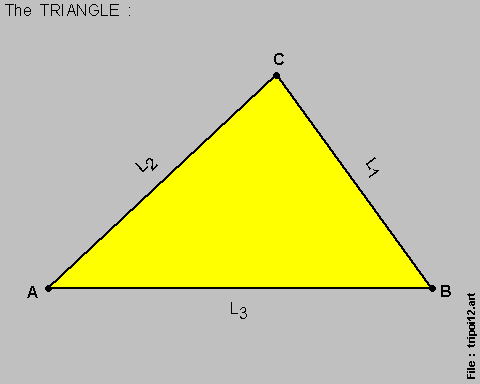
The following { inequalities } then always hold true , for any Triangle :

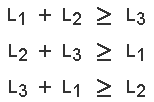
Let us now identify the { mid-points } of the 3 sides as { Point D } , { Point E } , & { Point F } respectively , as per this diagram below :

The lines { Line A-D } , { Line B-E } , & { Line C-F } do intersect at a single point , { Point P } as identified above , and this is the { Centroid } of the { Triangle } .

The significance of the { Centroid } is that :

• If we were to place 3 equal-mass's at the 3 vertices of the { Triangle } :
  • i.e. at { Point A } , { Point B } & { Point C } respectively ,

  then the { Center-of-Mass } would be at the { Centroid } of the { Triangle } , or { Point P } .

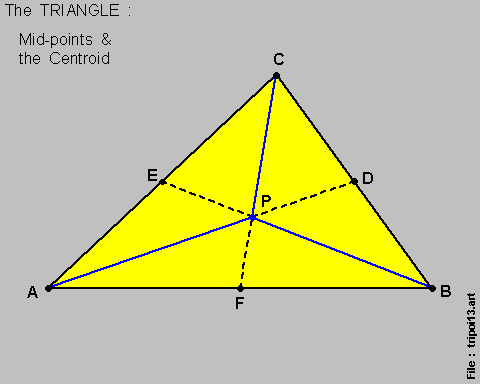
There is always a point that is { equi-distant } from the 3 vertices , as identified by { Point P } in this diagram below :

And this point is usually identified via the following procedure :

• We first identify the { mid-points } for the 3 sides , i.e. { Point D } , { Point E } & { Point F } respectively ,

• We then contruct { lines } perpendicular to the 3 sides passing thru the { mid-points } ,
  • { Line P-D } is perpendicular to { Line B-C } ,
  • { Line P-E } is perpendicular to { Line C-A } , &
  • { Line P-F } is perpendicular to { Line A-B } .

• And these 3 lines do intersect at a single point , { Point P } , the { Equi-distant Point } .

We also note here , in passing , that :

• { Triangle A-P-B } , { Triangle B-P-C } , & { Triangle C-P-A } are { isosceles triangles } .

Let us now construct 3 { lines } bisecting the 3 { angles } of the { Triangle } , as per this diagram below :

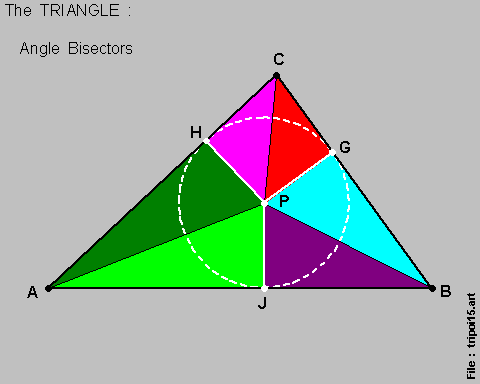
And these 3 { lines } do intersect at a single point , { Point P } as shown above .

Let us now 'drop' , from { Point P } , perpendicular lines to the 3 { sides } so that :

• { Line P-G } is perpendicular to { Line B-C } ,
• { Line P-H } is perpendicular to { Line C-A } , &
• { Line P-J } is perpendicular to { Line A-B } .

Noting that { Line A-P } , { Line B-P } & { Line C-P } are { angle bisectors } , it immediately follows that :

• { Triangle H-A-P } & { Triangle J-A-P } are congruent triangles ,
• { Triangle J-B-P } & { Triangle G-B-P } are congruent triangles , &
• { Triangle G-C-P } & { Triangle H-C-P } are congruent triangles .

so that { Line P-G } , { Line P-H } & { Line P-J } are { of-equal-lengths } .

As such , { Point P } is then the { center } for the { Inscribing Circle } , as marked above .

Let us now 'drop' , from each of the 3 vertices , perpendicular lines to the { Opposite Sides } :

so that :

• { Line A-K } is perpendicular to { Line B-C } ,
• { Line B-L } is perpendicular to { Line C-A } , &
• { Line C-M } is perpendicular to { Line A-B } .

These 3 { lines } do intersect at a single point , { Point P } , as marked in the diagram above .

The significance of this { point } shall be discussed later in { Section IV } , when we move-on to the { Congruent-Triangles Tetrahedron } .

The { Fermat Point } is the point where the { sum of the distances to the 3 vertices } is { at-a-minimum } .

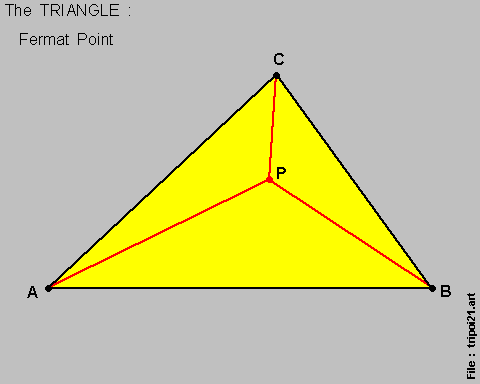
We shall simply mention here a special property for the { Fermat Point } , as identified by { Point P } in the above diagram :

• The three (3) angles , { angle B-P-C } , { angle C-P-A } , & { angle A-P-B } are equivalent ,
  • each being { 120 degrees } , or { ( 2 * PI / 3 ) radians } .

The { Fermat Point } is usually identified via the following procedure :

• We first construct three (3) { equilateral triangles } attached each of the original 3 { sides } ,

  and we identify the { outer-vertex } for each of the 3 { equilaterial triangles } as { Point U } , { Point V } , & { Point W } respectively ,

as per this diagram below :

• We then join the end-points to form the lines { Line A-U } , { Line B-V } & { Line C-W } respectively .

• These 3 { lines } do intersect at a single point , { Point P } , as identified above ,
  • and this is the { Fermat Point } .

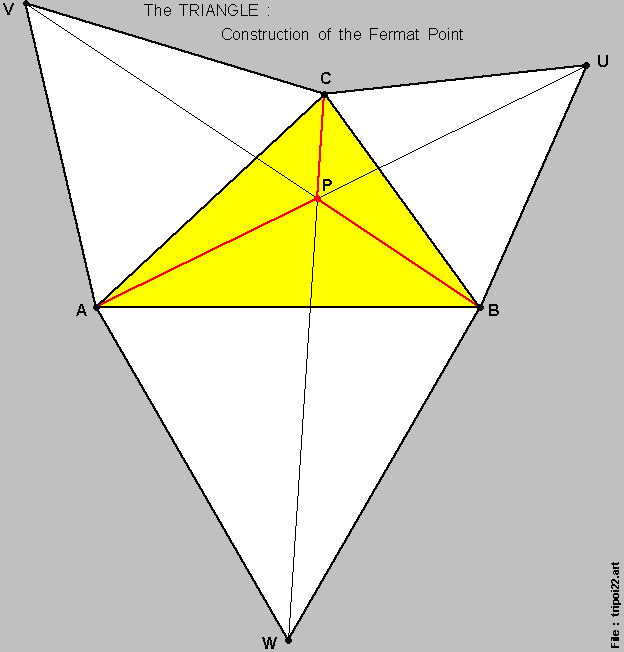
We shall have a more detailed discussion on this in Section VI --- An Infinite Series of { Triangles } .