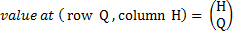On Unique-Factorization Combinatorics via the Pascal Triangle

by Frank C. Fung ( 1st published in October, 2012. )

Top Of Page

Section XIX - Creating the 10 x 10 [ ETA Matrix ]

Summary for the Section :

• In this Section , we shall create the 10 x 10 [ ETA Matrix ] .

go to Top Of Page

Creating the [ ETA Matrix ] :

• Let us bring-in again the 11 x 11 [ PASCAL Matrix ] from Section XVII and :
  • transpose the said Matrix to arrive at the [ Transposed PASCAL Matrix ] ,
    • as per the diagram on-the-right below .

  

• Let us now mark-off on the [ Transposed PASCAL Matrix ]
  • the 10 x 10 area we shall be duplicating for 10 x 10 [ ETA Matrix ] ,
    • as per the diagram on-the-right below .

  

• We then create the 10 x 10 [ ETA Matrix ] accordingly ,
  • as per the diagram-on-the-left below.

  

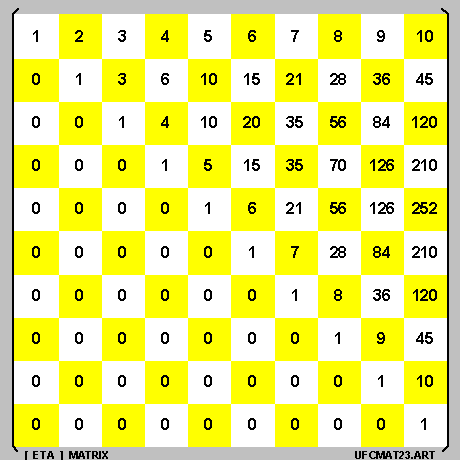
  And what we have done here essentially is to :

  • take-out the [ 1st row ] and the [ 1st column ] of the [ Transposed PASCAL Matrix ] .

go to Top Of Page

What is the [ ETA Matrix } :

• Let us just state here that :
  • For the position at { Row [ Q ] , Column [ H ] } of the [ ETA Matrix ] :
    • the value at the position is given by :
      • 

    And that-is-to-say :

    • the value here is simply the [ number of combinations ]
      • for { [ H ] things } taken { [ Q ] at-a-time } .

go to Top Of Page

go to the next section : Section XX - Creating the 10 x 10 [ Z Matrix ]

go to the last section : Section XVIII - Creating the 10 x 10 [ ALPHA Matrix ]

return to the Unique-Factorization Combinatorics HomePage

Original dated 2012-10-08