On Unique-Factorization Combinatorics via the Pascal Triangle

by Frank C. Fung ( 1st published in October, 2012. )

Top Of Page

Section II - The Pascal Triangle via Binomial Expansions

Summary for the Section :

• In this Section , we shall go thru the development process for the Pascal Triangle
  • via the expansion of Binomial Co-efficients .

go to Top Of Page

Binomial Expansion revisited :

• In general , a binomial is the sum of 2 terms .

  And the [ binomial ] that we shall be using here is :

  • [ z ] = ( x + y )

  Let us now take a quick look at the { powers-of-[ z ] } via the expansion of the [ binomial ] .

  • For [ z ] raised to the power-of-[ zero ] , we have :
    • 

  • For [ z ] raised to the power-of-[ 1 ] , we have :
    • 

  • For [ z ] raised to the power-of-[ 2 ] , we have :
    • 

  • For [ z ] raised to the power-of-[ 3 ] , we have :
    • 

  • For [ z ] raised to the power-of-[ 4 ] , we have :
    • 

  • For [ z ] raised to the power-of-[ 5 ] , we have :
    • 

  • For [ z ] raised to the power-of-[ 6 ] , we have :
    • 

  • and so-on-and-so-forth .

• And the Binomial Co-efficients for each { power-of-[ z ] } is then recorded
  • in the Pascal Triangle as shown below .

  

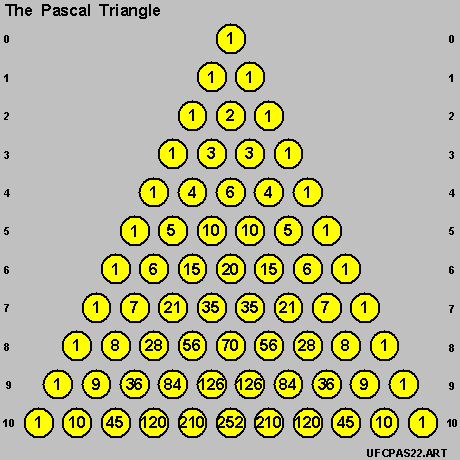
  • with each row of the Pascal Triangle recording the co-efficients
    • for a specific { power-of-[ z ] } .

  And the Pascal Triangle can be expanded downwards indefinitely

  • for further successive { powers-of-[ z ] } .

go to Top Of Page

General Formula for Binomial Expansions :

• And we list here , for the record , the general formula for Binomial Expansions :
  • 

  or alternately in this format using combinatorics notations :

  • 

go to Top Of Page

go to the next section : Section III - A Special Property of the Pascal Triangle

go to the last section : Section I - Introduction

return to the Unique-Factorization Combinatorics HomePage

Original dated 2012-10-08