On Unique-Factorization Combinatorics via the Pascal Triangle

by Frank C. Fung ( 1st published in October, 2012. )

Top Of Page

Section III - A Special Property of the Pascal Triangle

Summary for the Section :

• In this Section , we shall take quick look at the Additive Nature of the Pascal Triangle .

go to Top Of Page

The Additive Nature of the Pascal Triangle :

• Let us bring-in again the Pascal Triangle from the last Section ,
  • as per the diagram on-the-left below .

  And we take note here that :

  • For each row on the Pascal Triangle ,
    • the 1st element of the row is always a [ 1 ] ,

      and

    • the last element of the row is always a [ 1 ] ;

      as marked-off in [ red-color ] in the diagram on-the-right below .

  

• Let us now define , for our purpose immediately below ,
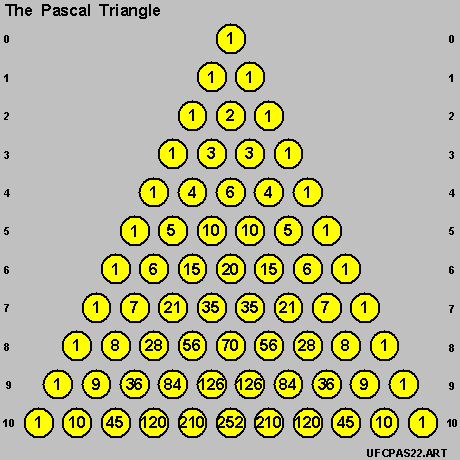
  • an [ Internal Element ] on the Pascal Triangle as :
    • any [ element ] on a row other than the [ 1st element ] or the [ last element ] on the row .

  And we are now ready to take a quick look at the Additive Nature of the Pascal Triangle ,

  • namely that :
    • for each [ Internal Element ] on a row , its value is always :

      the sum of the 2 [ elements ] on the row immediately above it closest to it .

• A few examples for quick demonstration here :
  • For the [ cyan-color ] pair marked-off in the diagram on-the-right above , we have :
    • [ 10 ] = [ 4 ] + [ 6 ]

  • For the [ green-color ] pair marked-off in the diagram on-the-right above , we have :
    • [ 70 ] = [ 35 ] + [ 35 ]

  • For the [ magenta-color ] pair marked-off in the diagram on-the-right above , we have :
    • [ 120 ] = [ 84 ] + [ 36 ]

go to Top Of Page

The Circumstances giving rise to this Special Property :

• Let us quick demonstrate why this is so .

  And we bring-in again this expansion for { [ z ] raised-to-the-5th-power } :

  • 

  And we take note here that the co-efficients for { [ z ] raised-to-the-4th-power } are :

  • [ 1 / 4 / 6 / 4 / 1 ] .

    so that we can now write :

  • 

  Consequently on expansion , we have :

  • 

    

    yielding :

  • 

    

  And on consolidating terms , we have :

  • 

    

  And we take special note here that the co-efficients in the above equation are :

  • [ 1 / ( 4 + 1 ) / ( 6 + 4 ) / ( 4 + 6 ) / ( 1 + 4 ) / 1 ]

  And the final equation here is of course :

  • 

• What we have demonstrated above then is that :
  • For any given row in the Pascal Triangle ,
    • the value of elements on the row can always be expressed as
      • the sum of 2 adjacent elements on the row immediately above .

  And the general equation giving rise to this phenomenon is then :

  • 

    yielding :

  • 

    and therefore the Additive Nature on a row-by-row basis .

• And to ensure our fullest understanding of the above phenomenon , we also provide herewith :
  • a [ counter-example ] via this set of 2 equations :
    • 

      yielding :

    • 

  And we see here that the [ Additive Nature ] of the Pascal Triangle will not work under such circumstances ,

  • simply because we did not start-out with the original [ binomial ] :
    • [ z ] = ( x + y )

go to Top Of Page

The Importance of this Special Property :

• The significance of this Special Property lies in the fact that :
  • each row of the Pascal Triangle can be constructed via the row immediately above it ,
    • using an [ addition-type ] procedure .

  Therefore , in the construction of the Pascal Triangle ,

  • the above-said [ Additive Nature ] will then permit us to bypass :
    • using the [ Factorials of Natural Numbers ]

      and

    • further processing via multiplications and/or divisions ;

    in the calculating the values of [ internal elements ] of each successive row .

• In Section XX of this paper , we shall be coming up with another version of the Pascal Triangle .

  It is therefore important that :

  • we are fully familiar with the mechanics of the Pascal Triangle
    • ahead of things-to-come .

go to Top Of Page

go to the next section : Section V - Setting up for the Calculations to follow in the next 10 Sections

go to the last section : Section II - The Pascal Triangle via Binomial Expansions

return to the The Unique-Factorization Combinatorics HomePage

Original dated 2012-10-08