An Approach to the Triangle

The { Fermat Point } of a triangle is the point where { sum of the distances to the 3 vertices } is at-a-minimum .

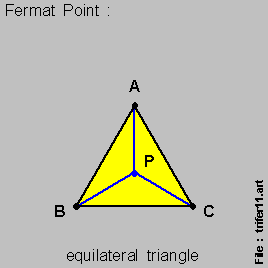
• For an { equilateral trinagle } , the { Fermat Point } is at the { centroid } , as per this diagram below :

  

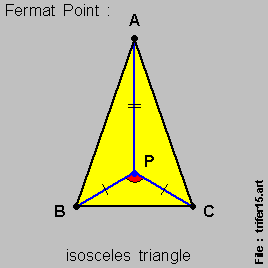
• For an { isosceles triangle } , the { Fermat Point } , { Point P } , is equi-distant from the 2 { base-line points } , { Point B } & { Point C } ,
  • with the angle { angle B-P-C } being [ 120 degrees ] , as per this set of 3 diagrams below :

  

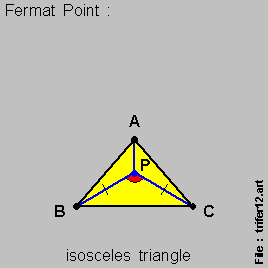
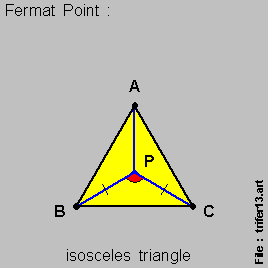
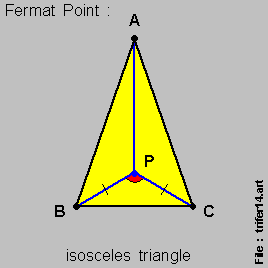
  And derivation here via modern-day { Differential Calculus } analysis is quite straight-forward .

  We then take note that the { Fermat Point } , { Point P } does not move as we move { Point A } along the { Line P-A } direction .

Let us now look at this set of 3 diagrams below where the { diagram on-the-left } & the { diagram on-the-right } are { isosceles triangles } .

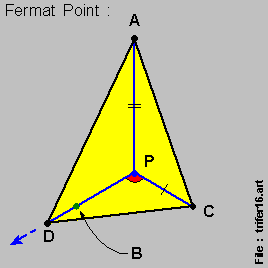
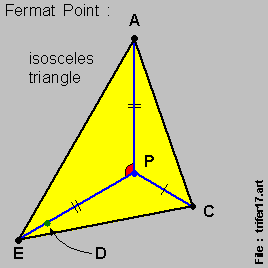
• For the { diagram in-the-middle } , { Point D } is a point bewteen { Point B } & { Point E } along the { Line P-B-E } direction ,

  And the { Fermat Point } , { Point P } , also remains unmoved & stationary in all the 3 diagrams .

  The derivation here via modern-day { Differential Calculus } analysis is slightly more complicated .

The { Fermat Point } , therefore , represents a good choice for a { point } for referencing the { Triangle } ,

• because its 3 { tri-axil directions } is always [ 120 degrees ] apart .

Let us now look at the { Fermat Point Construction Method } as applied to { Triangle D-E-F } :

• with { Triangle E-G-F } , { Triangle F-H-D } & { Triangle D-I-E } being the 3 { equilateral triangles } , as per the diagram on-the-left , below :

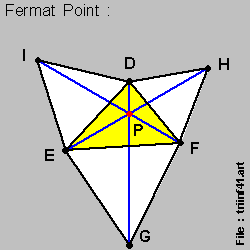
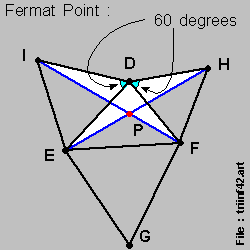
We note here a very special property , that :

• { Line D-G } , { Line E-H } & { Line F-I } are of-equal-lengths ,

and this is because :

• { Triangle I-D-F } & { Triangle E-D-H } are congruent triangles ,
• { Triangle G-E-D } & { Triangle F-E-I } are congruent triangles ,
• { Triangle H-F-E } & { Triangle D-F-G } are congruent triangles .

And we have marked-off { Triangle I-D-F } & { Triangle E-D-H } , the 1st set of { congruent triangles } , on the diagram on-the-right , above , for better clarity .

We simply note here that :

• { Line I-D } & { Line E-D } are of-equal-lengths , because of { equilateral triangle D-I-E } ,
• { Line D-F } & { Line D-H } are of-equal-lengths , because of { equilateral triangle F-H-D } ,
• { Angle I-D-F } & { Angle E-D-H } are equal , because both are equal to [ { Angle E-D-F } + 60 degrees ] ,

so that :

• { Triangle I-D-F } & { Triangle E-D-H } are congruent triangles , and
• { Line I-F } & { Line E-H } are therefore of-equal-lengths .

We then apply the same logical sequence to either of the other 2 sets of { congruent triangles } to arrive at the conclusion that :

• { Line D-G } , { Line E-H } & { Line F-I } are of-equal-lengths .