An Approach to the Triangle

For a triangle in general , { Triangle D-E-F } , we found that :

• when we apply the traditional { Fermat Point Construction Method } of attaching 3 { equailateral triangles } to the 3 sides ,

  the { centroids } of the 3 { equilateral triangles } forms another { equilateral triangle } , { Triangle R-S-T } .

The { centroids } of { Triangle D-E-F } & { Triangle R-S-T } are one-and-the-same point ,

• and we shall outline the proof here in this Appendix .

We then start-off with an { Isosceles Triangle } , { Triangle D-E-F } as shown in the diagram on-the-left , below :

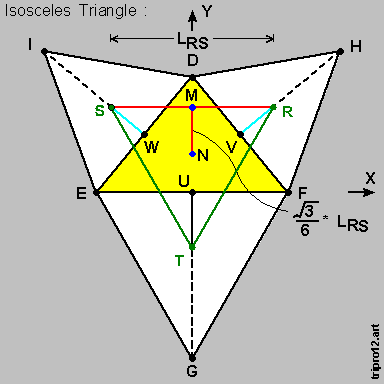
We then identify { Point U } as the mid-point of the { base-line } ,

• and use this as the { reference point } and set up our { X-Axis / Y-Axis } co-ordinate system therefrom .

The { centroid } of { Triangle D-E-F } is then { up one-third-the-height along Line U-D } , as marked .

Our proof then runs as follows :

• We first calculate the co-ordinates of the other mid-points , { Point V } & { Point W } ,
  • based on the { Height } & { L-Base } .

• We then calculate the co-ordinates of { Point R } & { Point S } ,

• We then calculate the co-ordinates of { Point M } , the mid-point of { Line R-S } ,

• We then calculate the co-ordinates of { Point N } , the { centroid } of { Triangle R-S-T } , with :
  • { Line M-N } being perpendicular to { Line R-S } , &
  • the { length of Line M-N } being { root-[ 3 ]-over-[ 6 ] } of the { length of Line R-S } .

And we will find that the co-ordinates of { Point N } co-incides with those of the { centroid } of { Triangle D-E-F } .

Let us now move { Point D } to-the-right by a distance { Delta } , as per the diagram on-the-left , below :

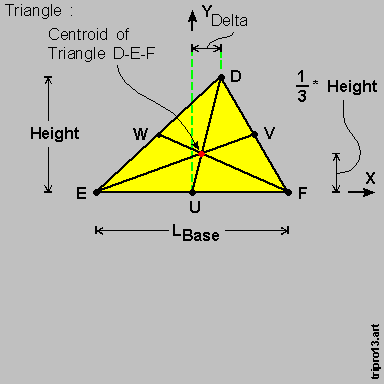
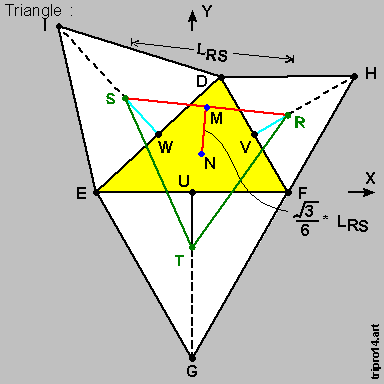
The { centroid } of { Triangle D-E-F } then moves horizontally by a distance equal to [ one-third times { Delta } ] .

Our proof then runs , again , as follows :

• We first calculate the co-ordinates of the other mid-points , { Point V } & { Point W } ,
  • based on the { Height } , { L-Base } & { Delta } .

• We then calculate the co-ordinates of { Point R } & { Point S } ,

• We then calculate the co-ordinates of { Point M } , the mid-point of { Line R-S } ,

• We then calculate the co-ordinates of { Point N } , the { centroid } of { Triangle R-S-T } , with :
  • { Line M-N } being perpendicular to { Line R-S } , &
  • the { length of Line M-N } being { root-[ 3 ]-over-[ 6 ] } of the { length of Line R-S } .

And we will find that the co-ordinates of { Point N } co-incides with those of the { centroid } of { Triangle D-E-F } .

This then completes our proof .