An Approach to Mathematic Functions Basics

by Frank C. Fung ( 1st published in December, 2014. )

Top Of Page

Section XXXII - Solving for [ R ] in terms of [ Theta ]

Summary for the Section :

• In this Section , we shall attempt to find a solution to this differential equation :
  • 

    this being the { Differential Equation involving [ R ] and [ Theta ] in its Second Format } from Section XXVIII .

go to Top Of Page

First Proposal for the format of the solution :

• Let us recall that :
  • For the Satellite moving in a [ Circular Orbit ] :
    • the equation here is :
      • 

    Let us now re-write this equation in this special format :

    • 

      for our comparison purposes immediately below .

  • For the [ Central Force disappearing totally ] and the Satellite therefore moving along in a [ Straight Line ] :
    • the equation here is :
      • 

  And based on the above two (2) special cases ,

  • our first proposal for a solution is then a function of the format :
    • 

      where :

      • 

  And we take special note at this point that :

  • for the [ Circular Orbit ] :
    • [ C = 1 ] and [ D = 0 ] .

  • for the [ Straight-Line Orbit ] :
    • [ C = 0 ] and [ D = 1 ] .

go to Top Of Page

Second Proposal for the format of a solution :

• Let us now take a closer look at our First Proposal above ,
  • i.e. the function of the format :
    • 

      where :

      • 

  Let us now re-write this equation immediately above in this format :

  • 

    yielding :

  • 

  And we see here that the this functional-relation can now be re-expressed in this equivalent format below :

  • 

    where :

    • 

• And this is the format of the functional-relation that we shall be using immediately below ,
  • to hash-out a solution to the { Differential Equation involving [ R ] and [ Theta ] in its Second Format } .

go to Top Of Page

Hashing-out the Solution :

• Let us now bring-in our Second Proposal :
  • 

    to serve as the core functional relation for our further review .

  And based on the above , the first-derivative of [ R ] with respect to [ Theta ] is then :

  • 

    yielding :

  • 

  And the second-derivative of [ R ] with respect to [ Theta ] is then :

  • 

    

    yielding :

  • 

• Let us now bring-in again the expression for [ R ] , i.e. :
  • 

  We then set up the following for our use immediately below :

  • 

  • 

  • 

• Let us now bring-in again the original { Differential Equation involving [ R ] and [ Theta ] } from above :
  • 

  Let us now evaluate each of the 3 terms on the left-hand-side , as follows :

  • for the [ 1st term ] :
    • We bring-in from above :
      • 

      and

      • 

      Therefore , the [ 1st term ] can now expressed as :

      • 

        yielding :

      • 

  • for the [ 2nd term ] :
    • We bring-in from above :
      • 

      and

      • 

      Therefore , the [ 2nd term ] can now be expressed as :

      • 

        yielding :

      • 

      And consequently ,

      • 

  • for the [ 3rd term ] :
    • We simply have :
      • 

      and consequently :

      • 

• Then , for the original { Differential Equation involving [ R ] and [ Theta ] } from above :
  • 

  we now have the following for the 3 terms on the left-hand-side :

  • 

  • 

  • 

  And on substituting there-in and consolidating terms , the Differential Equation now becomes :

  • 

    yielding :

  • 

• Let us stop here on this equation for a brief moment of reflection ,
  • because there are two (2) routes we can take on this equation .

go to Top Of Page

Taking the First Route on the Equation :

• Let us bring-in again the equation from immediately above :
  • 

  And on cancelling terms on the left-hand-side , we have :

  • 

  Therefore :

  • 

• And we can also express the quantity [ A ] via :
  • 

go to Top Of Page

Taking the Second Route on the Equation :

• Let us bring-in again the said equation-of-concern from above :
  • 

  Separating terms on the left-hand-side then yields us this :

  • 

• Let us recall that we have defined [ R ] above as :
  • 

  Therefore :

  • 

  Substituting this into equation immediately preceding , i.e. this equation :

  • 

  would then yield us this relation :

  • 

• Let us recall at this point that :
  • for our { Standardized Set of Initial Conditions } , we have at [ t = 0 ] :
    • 

    noting here of course that :

    • 

  Thus , the equation we have above , i.e. this equation :

  • 

  would turn into this equation below :

  • 

    when the { Initial Conditions } at [ t = 0 ] are applied to it .

  Consequently , we have :

  • 

• Let us bring-in , at this point , this result from the { First Route on the Equation } above :
  • 

  Substituting this into the equation immediately above then yields us this relation :

  • 

  And on re-arranging terms , we have :

  • 

  Consequently :

  • 

    yielding :

  • 

  Therefore :

  • 

go to Top Of Page

Expressing [ A ] and [ B ] in terms of [ R-sub-zero ] and [ V-sub-zero ] :

• Now that we have expressions for both [ A ] and [ B ] , i.e. the expressions :
  • 

  • 

  we shall now proceed to put these into a more precise format for our further evaluation .

• Let us recall at this point the definition of [ K ] from Section XXVI :
  • 

  Let us re-write this as :

  • 

    yielding :

  • 

  Let us recall that a [ t = 0 ], we have :

  • 

    and

  • 

  Consequently , we can now express [ K ] in terms of [ R-sub-zero ] and [ V-sub-zero ] via :

  • 

• And for our expression for [ B ] above , i.e. this expression :
  • 

  we can now re-write this as :

  • 

    yielding :

  • 

• And for our expression for [ A ] from above , i.e. this expression :
  • 

  we can now re-write this as :

  • 

    yielding :

  • 

go to Top Of Page

The final format for expressing [ R ] in terms of [ Theta ] :

• Let us recall our second proposal for the solution from above , i.e. this equation :
  • 

  Substituting the expresssions for [ A ] and [ B ] therein then yields us this :

  • 

  Consequently :

  • 

• Let us now re-write this equation in this special format :
  • 

    thereby yielding this final equation :

  • 

• Let us now bring back the single type of equation we have developed in Section XXIII for the Circle-Ellipse-Parabola-Hyperbola ,
  • i.e. , this equation :
    • 

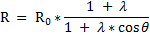
    for a quick comparison .

  Striking similarity here , I wound say !

go to Top Of Page

go to the next section : Section XXXIII - Summarizing on the Orbits of a Satellite

go to the last section : Section XXXI - The Case of the Central Force disappearing totally

return to the MATH Functions Basics HomePage

Original dated 2014-12-07