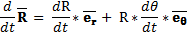An Approach to Mathematic Functions Basics

by Frank C. Fung ( 1st published in December, 2014. )

Top Of Page

Section XXVI - Setting up the Polar Co-ordinates Reference Frame

Summary for the Section :

• In this Section , we shall do the following :
  • set up the general [ reference frame ] for our use in the remainder of Part VI ,

  • set up the { Position / Velocity / Acceleration Vectors } for the Satellite in Polar Co-ordinates .

go to Top Of Page

Setting up the { Reference Frame } and the { Polar Co-ordinates System } :

• Let us first set up a { U-V Axis Co-ordinate System } in a 2 Dimensional Plane ,
  • with the [ Point-of-Origin ] here being the point [ Point O ] ,
    • as marked-off in the diagram on-the-left below .

  

• We then identify the position of the Satellite at any time [ t ] via the point [ Point P ] ,
  • so that :
    • the position of the Satellite at any time [ t ] can be clearly-and-precisely defined by the Position Vector [ Vector O-P ] .

  And the Position Vector [ Vector O-P ] at any time [ t ] is defined in the { Polar Co-ordinates System } via :

  • the distance [ R ] ,
    • being the distance of the [ Line-Segment O-P ] ; and

  • the angle [ Theta ] ,
    • being the angle in-between the [ Vector O-P ] and the [ U-Axis ] ;

    as shown in the diagram on-the-left , above .

go to Top Of Page

Setting up the 2 [ unit vectors ] :

• Let us also set up , at this point , the two (2) unit-vectors :
  • the unit-vector [ Vector e-sub-R ] and the unit-vector [ Vector e-sub-Theta ] ,
    • as shown in the diagram on-the-right above ;

    with :

    • the unit-vector [ Vector e-sub-R ] here being in the [ O-P direction ] ,

      and

    • the unit-vector [ Vector e-sub-Theta ] being orthogonal to [ Vector e-sub-R ] as shown .

  And the first-derivatives of the said 2 Unit-Vectors with respsect to time are then :

  • 

    and

  • 

go to Top Of Page

The Position Vector for the Satellite :

• The Position Vector for the Satellite at any time [ t ] is then expressed as :
  • 

go to Top Of Page

The Velocity Vector for the Satellite :

• And the Velocity Vector of the Satellite is then expressed as :
  • 

go to Top Of Page

The Acceleration Vector for the Satellite :

• The Acceleration Vector of the Satellite is then expressed as :
  • 

  And on consolidating terms , we have the Acceleration Vector in this format :

  • 

• And we take special note at this point of this general relation :
  • 

  Dividing throughout by [ R ] then yields us this equation :

  • 

  Let us now substitute this back into the equation we have immediately above for the Acceleration Vector and we have :

  • 

go to Top Of Page

Satellite moving under a Central Force :

• Let us assume for the time-being that the Satellite is moving under the influence of a Central Force ,
  • with the Force Center here being at the Point-Of-Origin ,
    • i.e. , the point [ Point O ] .

  Under such circumstances :

  • the component of the Acceleration Vector for the Satellite in the [ e-sub-Theta ] direction is necessarily [ zero ] .

• Consequently , we can now write :
  • 

  And for { [ R ] being not equal to [ zero ] } , we have :

  • 

  As a result :

  • 

go to Top Of Page

go to the next section : Section XXVII - Setting up Central Force influencing the Satellite

go to the last section : Section XXV - A Statement of Purpose for Part VI

return to the MATH Functions Basics HomePage

Original dated 2014-12-07