An Approach to Mathematic Functions Basics

by Frank C. Fung ( 1st published in December, 2014. )

Top Of Page

Section XXXIV - Other Central Forces of a Similar Nature

Summary for the Section :

• In this Section , we shall look at the Orbit of a Satellite moving under a Central Force ,
  • with the Central Force in-question here being a Gravitation-Type Force
    • varying as the { inverse of [ R-raised-to-the-Nth-Power ] } ,

    i.e. :

    • 

go to Top Of Page

A Quick Comment on the Gravitation Constant :

• Let us quickly look at a few examples of the different types of Gravitational Force we shall be studying here :
  • For the Central Force varying as the [ inverse of R-square ] , we have :
    • 

  • For the Central Force varying as the [ inverse of R-cube ] , we have :
    • 

  • For the Central Force varying as the [ inverse of R-raised-to-the-fourth-power ] , we have :
    • 

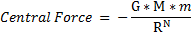
  And we simply take note here that the units for [ G-sub-2 ] , [ G-sub-3 ] and [ G-sub-4 ] will be different .

• In general ,
  • for the Central Force varying as the [ inverse of R-raised-to-the-Nth-power ] , we shall use :
    • 

      where :

      • [ G-sub-N ] is the Gravitaion Constant bearing the appropriate units.

go to Top Of Page

Setting up the Differential Equations :

• We simply state here that :
  • For the Central Force varying as the [ inverse of R-raised-to-the-Nth-power ] ,
    • we can go thru the same procedure as we have outlined in Sections XXVI thru Section XXVIII

      to arrive at the [ differential equations ] .

• Let us just state the results for the said Central Force here , as follow :
  • the { Differential Equation with respect to time } is given by :
    • 

  • the { Differential Equation involving [ R ] and [ Theta ] } derived therefrom is given by :
    • 

    And on multiplying throughout by [ R-square over K-square ] , we have :

    • 

  And we take note here that :

  • the left-hand-side of corresponding Differential Equations are always the same ,

    but :

  • the right-hand-side do vary as the { inverse of increasing-powers-of-[ R ] } .

• let us now re-write the last equation immediately above in this special format :
  • 

    for our further study and analysis to follow .

go to Top Of Page

Taking note of a special relation :

• Let us set up , at this point , a special variable [ Q ] being :
  • the { first-derivative of [ R ] with respect to [ Theta ] } divided by [ R-Square ] ,

    i.e. :

    • 

  Taking the derivative thereof with respect to [ Theta ] then yields us this relation :

  • 

  And on re-arranging , we have :

  • 

  Therefore :

  • 

• Let us now bring-in this equation from above :
  • 

    this being the { Differential Equation involving [ R ] and [ Theta ] }

    • for the Central Force varying as the { inverse of [ R-raised-to-the-Nth-Power ] } .

  We notice at this point that :

  • the 1st and 2nd terms on the left-hand-side of this equation correspond exactly
    • to the right-hand-side of the equation immediately above .

  Consolidating the two (2) equations then yields us this relation :

  • 

    for our further manipulation below .

go to Top Of Page

Setting up [ z ] as the reciprocal of [ R ] :

• Let us now set up the variable [ z ] as the reciprocal of [ R ] , i.e. :
  • 

  Taking derivative with respect to [ Theta ] on both sides then yields us this relation :

  • 

  Consequently , we can now write :

  • 

• Let us now take a quick look at :
  • the { first-derivative of [ z ] with respect to [ Theta ] } ,

  and we have :

  • 

  Consequently :

  • 

  And on switching signs , we have :

  • 

• Let us now bring-in this equation from above :
  • 

    this being the derived { Differential Equation involving [ R ] and [ Theta ] }

    • for the Central Force varying as the { inverse of [ R-raised-to-the-Nth-Power ] } .

  Let us now re-write this equation in this special format below :

  • 

  Since we have defined [ z ] as :

  • 

    and also established immediately above :

  • 

  we can now substitute these into the equation immediately preceeding to arrive at this equation below :

  • 

  And on bringing the [ minus sign ] outside on the 1st term on the left-hand-side , we have :

  • 

  Consequently , we have :

  • 

• And this then is the final { Differential Equation involving [ z ] and [ Theta ] } ,
  • for the Central Force being a Gravitation-Type Force varying as the { inverse of [ R-raised-to-the-Nth-power ] } .

go to Top Of Page

go to the next section : Section XXXV - Re-doing the Differential Equation for [ N = 2 ]

go to the last section : Section XXXIII - Summarzing on the Orbit of a Satellite

return to the MATH Functions Basics HomePage

Original dated 2014-12-07