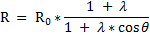An Approach to Mathematic Functions Basics

by Frank C. Fung ( 1st published in December, 2014. )

Top Of Page

Section XXXV - Re-doing the Differential Equation for [ N = 2 ]

Summary for the Section :

• In this Section , we shall take a more rigorous approach on :
  • solving the Differential Equation for [ N = 2 ] .

go to Top Of Page

Solving up the Differential Equation for [ N =2 ] :

• Let us bring back this general Differential Equation from the last Section :
  • 

    with :

    • 

  For [ N =2 ] , this equation would become :

  • 

    yielding :

  • 

• We take note here that this Differential Equation is of the format :
  • 

  and our proposed solution here is then :

  • 

  And :

  • the first-derivative thereof is then :
    • 

  • the second-derivative thereof is then :
    • 

  Let us now substitute these back into the orginal Differential Equation ,

  • i.e., this equation :
    • 

  and we have :

  • 

• And we see here that if we set :
  • 

    the above-said Differential Equation would indeed be satisfied .

  Thus , our proposed solution can now be re-written as :

  • 

    or alternately ,

  • 

• Since we have already established that :
  • 

    back in Section XXXII ;

  we can now write the above equation as :

  • 

    yielding :

  • 

  Further manipulations then yield us this equation :

  • 

  And consequently :

  • 814

• Let us now bring in the [ initial conditions ] at [ t = 0 ] , i.e. :
  • 

  The value of [ ONE-over-R ] at [ t = 0 ] is then given by :

  • 815

  And we see here that if set :

  • 

    the left-hand-side of the expression above would evaluate to { ONE-over-[ R-sub-zero ] } as required .

• And based on this , we shall now set :
  • 

  And our proposed solution would then become :

  • 

  And the final format of our solution here is :

  • 

• The question then arises as to whether this equation above does conform to :
  • the equations that we have for the Circle , Ellipse , Parabola and the Hyperbola ;

    i.e. , this type of equation from Part III / IV / V :

    • 

  And the answer here is YES , as explained below .

• Let us bring back the final equation above , i.e. :
  • 

  Let us do this simple munipulation below :

  • 

    to arrive at this equation :

  • 

  Consequently , we can now re-write the above equation in this format :

  • 

    to arrive at this final format for the same equation .

  • 

• And this equation does conform to the format we had orginally for the Circle , Ellipse , Parabola and the Hyperbloa .

go to Top Of Page

go to the next section : Section XXXVI - Doing the Differential Equation for [ N = 3 ]

go to the last section : Section XXXIV - Other Central Forces of a similar nature

return to the MATH Functions Basics HomePage

Original dated 2014-12-07