An Approach to Mathematic Functions Basics

by Frank C. Fung ( 1st published in December, 2014. )

Top Of Page

Section XXVII - Setting up the Central Force influencing the Satellite

Summary for the Section :

• In this Section , we shall place a [ point-mass of mass M ] at the Point-Of-Origin [ Point O ] ,
  • so that :
    • the said [ point-mass ] will exert a Gravitational Pull on the Satellite .

  And this then is our { system of a Satellite moving under a Central Force }

  • that we shall be investigating throughout the remainder of this [ Part V ] on :
    • the Orbit of a Satellite moving under a Central Force .

go to Top Of Page

Recalling the variables for the Position Vector :

• Let us recall that the core variables for the Position Vector are as follows :
  • 

  • 

  

go to Top Of Page

Setting up the variables for the Velocity Vector :

• Let us now also set up the variables [ V-sub-R ] and [ V-sub-Theta ] for the Velocity Vector .

  And we define :

  • 

  • 

    as per the diagram on-the-right above .

  And consequently , the Velocity Vector for the Satellite may be written in this manner :

  • 

• Let us bring back again , from the last Section , this equation for the Velcocity Vector :
  • 

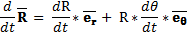
  And on equating the two (2) equations immediately above , we have :

  • 

  • 

go to Top Of Page

Setting up Gravity as the Central Force :

• Let us now place a [ point-mass of mass M ] at the Point-Of-Origin [ Point O ] ,
  • so that :
    • its position is fixed-and-invariant thru time .

  

  Consequently , the Gravitational Pull exerted by the said [ Point-Mass M ] on the satellite is given by :

  • 

    where :

    • 

    • 

    • 

    • 

  We can then express the { Force on the Satellite } , always in the radial-direction , as :

  • 

go to Top Of Page

Force Equilibrium Considerations for the Satellite :

• Let us now take a quick look at the Force Equilibrium situation for the Satellite at any time [ t ] ,
  • governed by :
    • Force = Mass x Acceleration

  We then have this equation below :

  • 

    in the format :

    • Mass x Acceleration = Force

  Let us now re-write the above equation in this manner below :

  • 

  Consequently :

  • 

  And what this equation tell us here is that :

  • 

    and the Acceleration is always in the [ radial direction ] .

• Let us now bring back this equation for the Acceleration Vector from the last Section :
  • 

  And on equating the force-equilibrium equations for the orthogonal [ e-sub-R ] and [ e-sub-Theta ] direction , we have :

  • for the [ e-sub-R ] direction :
    • 

  • for the [ e-sub-Theta ] direction :
    • 

• And of course , this last equation above does tell us again that :
  • 

  And as a result :

  • 

    same as before .

go to Top Of Page

Identifying the core Differential Equation :

• Let us bring-in again from above the Force Equilibrium equation in the [ e-sub-R ] direction :
  • i.e. this equation :
    • 

  We shall now identify this equation as :

  • the { core Differential Equation governing the behavior of the Satellite }
    • for our referencing purpose in the Sections to follow .

go to Top Of Page

What's Next :

• And with this core Differential Equation in-hand ,
  • we are now ready to derive therefrom :
    • the Differential Equation involving [ R ] and [ Theta ] .

  And we shall do so next .

go to Top Of Page

go to the next section : Section XXVIII - The Differential Equation involving [ R ] and [ Theta ]

go to the last section : Section XXVI - Setting up the Polar Co-ordinates Reference Frame

return to the MATH Functions Basics HomePage

Original dated 2014-12-07