An Approach to Mathematic Functions Basics

by Frank C. Fung ( 1st published in December, 2014. )

Top Of Page

Section XXII - Equation for the Parabola

Summary for the Section :

• In this Section , we shall derive the Equation for the Parabola in the { Polar Co-ordinates } :
  • i.e. , this equation :
    • 

  And we shall put the same equation into this very special format :

  • 

    for our comparison purposes use in the next Section ,

go to Top Of Page

Defining of the Parabola :

• In general , the Parabola is defined via its [ Focal Point ] and its [ Directrix ] :
  • with :
    • the [ Directrix ] here being any given straight-line on a 2-Dimensional Plane , and

    • the [ Focal Point ] here being any point in the said 2-Dimensional Plane not on the [ Directrix ] ;

    as shown in the diagram on-the-left below .

  

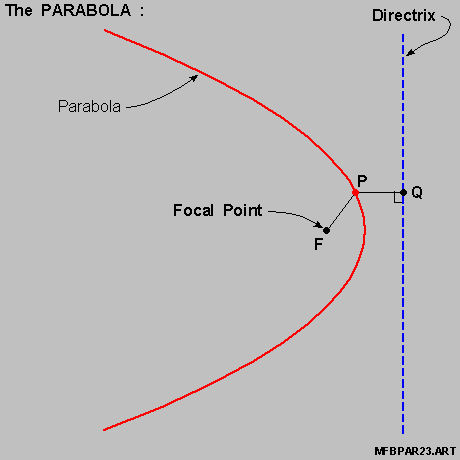
  And the Parabola is defined via :

  • IF :
    • the point [ Point P ] is a point on the Parabola ,

    THEN :

    • the distance from [ Point P ] to the [ Focal Point ]

      and

    • the perpendicular distance from [ Point P ] to the [ Directrix ]

      are equal .

• And we bring-in , at this point , a sample Parabola as per the diagram on-the-right above .

go to Top Of Page

Setting up the { U-V Axis Co-ordinate System } :

• Let us now set up the { U-V Axis Co-ordinate System } for our analysis to follow .

  FIRST ,

  • we set up the [ U-Axis ] via :
    • setting up a straight-line passing thru the [ Focal Point ] perpendicular to the [ Directrix ] ,
      • as shown in the diagram on-the-left below .

  SECOND :

  • we set up the [ V-Axis ] via :
    • setting up a straight-line passing thru the [ Focal Point ] perpendicular to the [ U-Axis ] .
      • as shown in the diagram on-the-left below .

  

  We can then mark-off the { perpendicular distance from the [ Focal point ] to the [ Directrix ] } as the distance [ D ] ,

  • i.e. :
    • 

go to Top Of Page

Deriving the Equation for the Parabola :

• Let us now derive the equation for the Parabola using the { Polar Co-ordinates System } .

  And in the { Polar Co-ordinate System } , the position of any point [ Point P ] is defined by the [ Position Vector F-P ] ,

  • which in turn is defined by the distance [ R ] and the angle [ Angle PSI ] ,
    • as per the diagram on-the-left below .

  

• Let us now set up , for any point [ Point P ] on the Parabola , the distance [ L1 ] and the distance [ L2 ] :
  • 

  • 

  And we always have :

  • 

    this being the defining relation for the Parabola .

• And based on the 2 diagrams above , we can now write :
  • for any point [ Point P ] on the Parabola :
    • 

    • 

  And equating the 2 distances then yields us this relation :

  • 

  Consequently :

  • 

  Therefore :

  • 

    yielding :

  • 

• And this equation immediately above is then :
  • the defining equation for the Parabola in { Polar Co-ordinates } .

go to Top Of Page

Identifying the Vertex and [ R-sub-zero ] :

• Let us now bring-in this set of 2 diagrams below , and :
  • mark-off the point [ Point G ] as the insection of the [ Parabloa ] and the [ U-Axis ] .

  

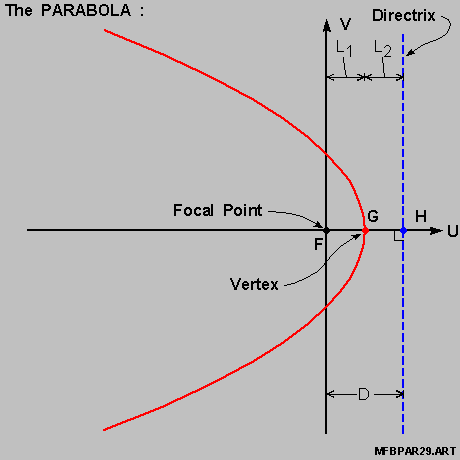
  And we take note here that [ Point G ] is in fact the Vertex of the Parabola ,

  • being the point on the Pararbola closest to the [ Focal Point ] .

• Let us briefly explain why this is so .
  • First , we bring back this equation from above expressing [ R ] in terms of the angle [ Angle PSI ] :
    • 

    And :

    • for the point [ Point G ] on the [ U-Axis ] , the value of [ Angle PSI ] is [ zero ] and :
      • 

    • for all other points on the Parabola other than [ Point G ] , we have :
      • 

  • This then tell us that :
    • [ R ] does attain its minimum value when [ PSI = 0 ] ;

    because :

    • the denominator on the right-hand-side of this equation :
      • 

        is at its maximum when [ PSI = 0 ] .

• Let us now mark-off the [ length of Line-Segment F-G ] as the distance [ R-sub-zero ] ,
  • i.e. :
    • 

      as shown in the diagram on-the-left above .

go to Top Of Page

Expressing [ D ] in terms of [ R-sub-zero ] :

• Let us now take a quick look at distances associated with the point [ Point G ] ,
  • and we bring-in again this set of 2 diagrams from above .

  

  For the [ length of Line-Segment F-G ] , we have :

  • 

  Since [ Point G ] is a point on the Parabola and therefore :

  • 

    the [ length of Line-Segment G-H ] is simply given by :

    • 

• And since [ Point F ] , [ Point G ] and [ Point H ] are all { points on the [ U-Axis ] } ,
  • and are therefore co-linear ;

  it then follows that :

  • 

    arising from :

    • [ length of Line-Segment F-G ] + [ length of Line-Segment G-H ] = [ length of Line-Segment F-H ]

• Substituing therein the values of [ L1 ] and [ L2 ] established immediately above then yield us this equation :
  • 

  And consequently , we have :

  • 

go to Top Of Page

Re-formatting the Equation for our use :

• Let us now bring back this equation from above :
  • 

  Substituting therein { D = 2*[ R-sub-zero ] } then gives us this :

  • 

    yielding :

  • 

  Let us now re-write this equation immediatley above in this special manner :

  • 

• And the final format of the same equation is then :
  • 

    for our comparison purposes to follow .

  And with this in hand , we are now ready to do :

  • the { Linkage System for the Circle / Ellipse / Parabola / Hyperbola } , next !

go to Top Of Page

go to the next section : Section XXIII - Linkage System for the Circle / Ellipse / Parabola / Hyperbola

go to the last section : Section XXI - Equation for the Circle

return to the MATH Functions Basics HomePage

Original dated 2014-12-07