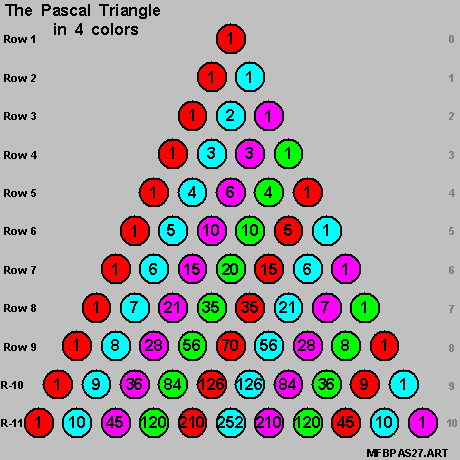
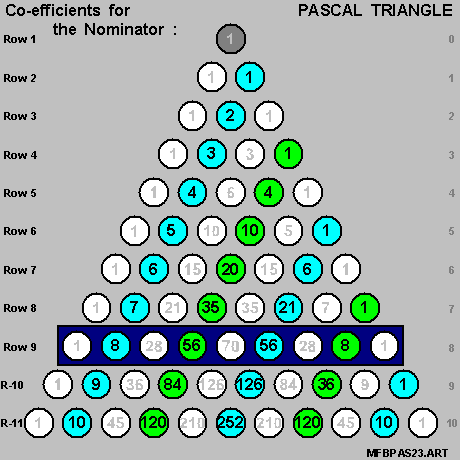
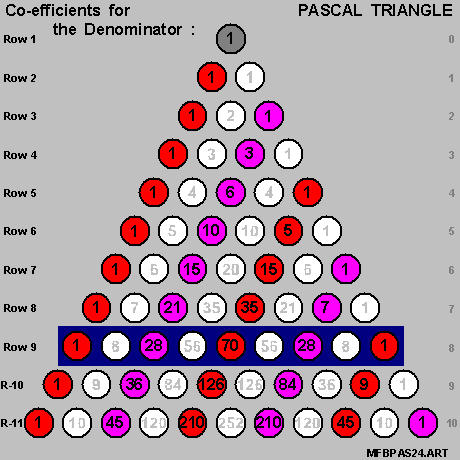
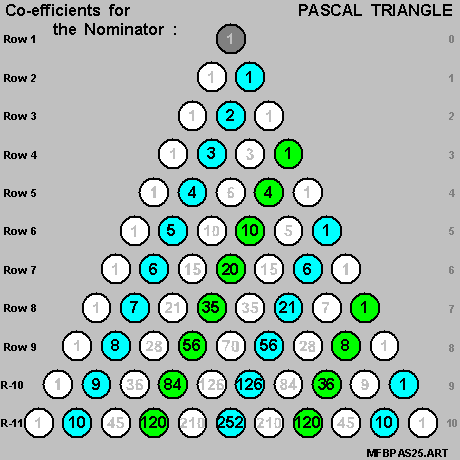
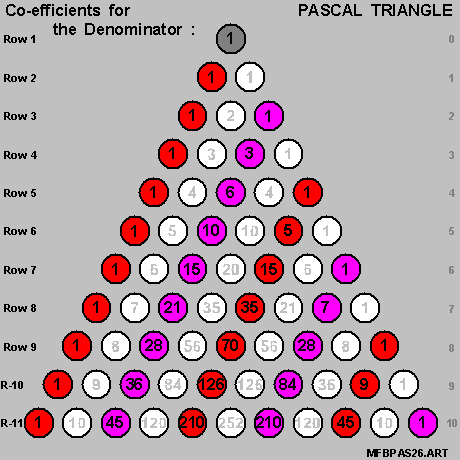
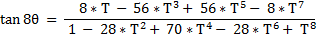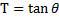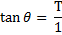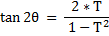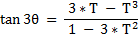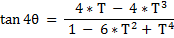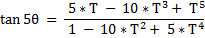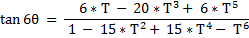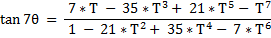- for the [ fraction ] expressing the { tangent of [ N*Theta ] } in terms of the { tangent of [ Theta ] } ,
- the co-efficients in the Nominator and the co-efficients in the Denominator
- are always members of the same row of the Pascal Triangle .
- the co-efficients in the Nominator and the co-efficients in the Denominator
And we shall also create the { 4-Colors Pascal Triangle } , as per the diagram on-the-right below , for our use in the next Section .