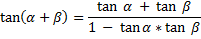An Approach to Mathematic Functions Basics

by Frank C. Fung ( 1st published in December, 2014. )

Top Of Page

Section XLI - Deriving the Tangent Addition Formula

Summary for the Section :

• In this Section , we shall go thru the derivation process for the Tangent Addition Formula ,
  • i.e. the formula :
    • 

go to Top Of Page

Setting-up [ Angle ALPHA ] , [ Angle BETA ] and [ Angle PSI ] :

• Let us first set up the 2 [ angles ] of our primary concern here , namely :
  • the angle [ Angle ALPHA ] and the angle [ Angle BETA ] repsectively .

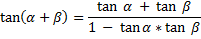
  We then set up the angle [ Angle PSI ] ,

  • 

    being the sum of [ angle ALPHA ] and [ angle BETA ] .

• For our derivation process to follow , we shall be working primarily with { Right-Angle Triangles } .

  And because of this , it is necessary for us to place certain restrictions on the size of the 3 angles :

  • Restriction ONE :
    • the angles [ Angle ALPHA ] , [ Angle BETA ] and [ Angle PSI ] are [ non-negative ] .

  • Restriction TWO :
    • [ Angle PSI ] is less than [ 90 degrees ] .

      ( This is a necessary restriction in order that the { tangent of PSI } may be expressable via a { right-angle triangle } ) .

  And as a consequent to these restrictions :

  • [ Angle ALPHA ] and [ Angle BETA ] must also less than [ 90 degrees ] .

• Let us now summarize the net effects of these restrictions as follows :
  • 

  • 

    and :

  • 

go to Top Of Page

Expressing the tangents of [ ALPHA / BETA / PSI ] via { Right-Angle Triangles } :

• let us now express the tangents of the 3 angles above via { Right-Angle Triangles } :
  • as per this set of three (3) diagrams below :

  

• For the diagram on-the-left above , we then have :
  • 

    and

  • 

• And :
  • for the diagram in-the-middle above , we have :
    • 

  Or alternately :

  • for the diagram on-the-right above , we have :
    • 

go to Top Of Page

Deriving the Tangent Addition Formula :

• Let us now bring-in this set of 3 diagrams for our use in the derivation process :

  

• Let us first identify the angle [ Angle TAU ] as the [ Angle E-C-D ] :
  • as per the diagram on-the-left above .

  We take note , at this point , that for the [ straight-line F-E-C-B ] passing thru [ Point C ] :

  • [ Angle E-C-D ] + [ Angle D-C-A ] + [ Angle A-C-B ] = [ 180 degrees ] .

    yielding :

  • 

  We also take note here that the 3 [ angles ] of [ Triangle A-C-B ] always add-up to [ 180 degrees ] , i.e. :

  • [ Angle B-A-C ] + [ Angle A-C-B ] + [ Angle C-B-A ] = [ 180 degrees ] .

    yielding :

  • 

  Combining the 2 equations above then yields us this relation :

  • 

    namely that the 2 angles [ Angle TAU ] and [ Angle ALPHA ] are equal-in-value .

• Let us now express the lengths [ L2 ] , [ L3 ] , [ L4 ] , [ L5 ] and [ L6 ] in terms of [ L1 ] :
  • For [ L2 ] and [ L3 ] , we have :
    • 

    • 

  • For [ L4 ] , we have :
    • 

    And substituting the value of [ L3 ] from above into this equation then yields us this :

    • 

  • For [ L5 ] and [ L6 ] , we have :
    • 

    • 

    Let us now substitute the value for [ L4 ] from above into these 2 equations :

    • noting here , of course , that [ Angle TAU ] and [ Angle ALPHA ] are equal-in-value .

    We then have :

    • 

    • 

    And on consolidating terms , we have :

    • 

    • 

• Let us recall the tangent of [ Angle PSI ] from above , using this alternate format :
  • 

  Expressing this in-terms-of [ L1 ] , [ L2 ] , [ L5 ] and [ L6 ] then yields us this equation :

  • 

  We can then substitute the values for [ L2 ] , [ L5 ] and [ L6 ] from above there-in to arrive at this :

  • 

  And on consolidating terms , we have :

  • 

• And this would then yield us , indeed , the Tangent Addition Formula :
  • 

go to Top Of Page

go to the next section : Section XLII - The Tangent Addition Formula in Action

go to the last section : Section XL - A Statement of Purpose for Part VI

return to the MATH Functions Basics HomePage

Original dated 2014-12-07