

but excluding the solution-value [ 1 ] .
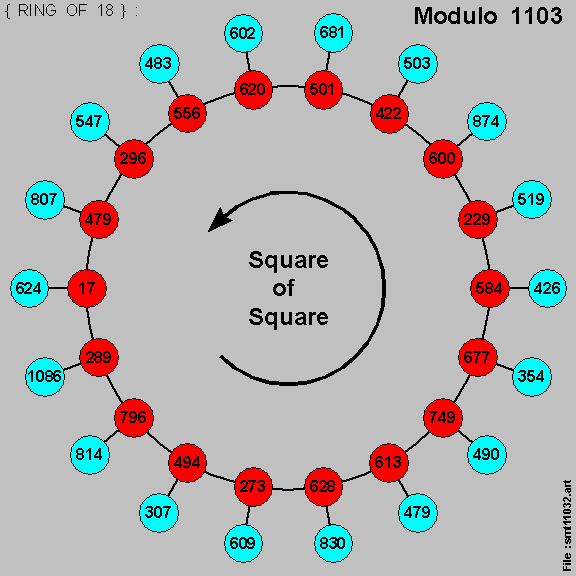

but excluding the solution-value [ 1 ] .

In the Section , we shall construct a { Multiplication Table } for [ modulo 1103 ] ,
For the { prime number } [ P ] being equal to [ 1,103 ] , we set up the corresponding value [ Q ] such that :
And we can write :
We can then set-up the { core elements } for building the { Multiplication Table } for [ modulo 1103 ] , as follows :
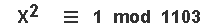


but excluding the solution-value [ 1 ] .


but excluding the solution-value [ 1 ] .

We can then construct the { Multiplication Table } for [ modulo 1103 ] as follows :
| 1 | 2 | 4 | 16 | 256 | 459 | 8 | 64 | 787 | 586 | 363 | 512 | 733 | 128 | 942 | 552 | 276 | 69 | 349 | 471 | 138 | 293 | 918 | 32 | 1024 | 726 | 945 | 698 | 781 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 4 | 16 | 256 | 459 | 8 | 64 | 787 | 586 | 363 | 512 | 733 | 128 | 942 | 552 | 276 | 69 | 349 | 471 | 138 | 293 | 918 | 32 | 1024 | 726 | 945 | 698 | 781 | |
| 17 | 17 | 34 | 68 | 272 | 1043 | 82 | 136 | 1088 | 143 | 35 | 656 | 983 | 328 | 1073 | 572 | 560 | 280 | 70 | 418 | 286 | 140 | 569 | 164 | 544 | 863 | 209 | 632 | 836 | 41 | |
| 289 | 289 | 578 | 53 | 212 | 83 | 291 | 106 | 848 | 225 | 595 | 122 | 166 | 61 | 593 | 900 | 696 | 348 | 87 | 488 | 450 | 174 | 849 | 582 | 424 | 332 | 244 | 664 | 976 | 697 | |
| 796 | 796 | 489 | 978 | 603 | 824 | 271 | 853 | 206 | 1051 | 990 | 1065 | 545 | 1084 | 412 | 895 | 398 | 199 | 877 | 951 | 999 | 651 | 495 | 542 | 103 | 1090 | 1027 | 1077 | 799 | 687 | |
| 494 | 494 | 988 | 873 | 183 | 722 | 631 | 643 | 732 | 522 | 498 | 636 | 341 | 318 | 361 | 985 | 247 | 675 | 996 | 338 | 1044 | 889 | 249 | 159 | 366 | 682 | 169 | 261 | 676 | 867 | |
| 273 | 273 | 546 | 1092 | 1059 | 399 | 668 | 1081 | 927 | 869 | 43 | 932 | 798 | 466 | 751 | 167 | 688 | 344 | 86 | 419 | 635 | 172 | 573 | 233 | 1015 | 493 | 761 | 986 | 838 | 334 | |
| 628 | 628 | 153 | 306 | 121 | 833 | 369 | 612 | 484 | 92 | 709 | 746 | 563 | 373 | 968 | 368 | 314 | 157 | 315 | 778 | 184 | 630 | 906 | 738 | 242 | 23 | 389 | 46 | 453 | 736 | |
| 613 | 613 | 123 | 246 | 984 | 302 | 102 | 492 | 627 | 420 | 743 | 816 | 604 | 408 | 151 | 577 | 858 | 429 | 383 | 1058 | 840 | 766 | 923 | 204 | 865 | 105 | 529 | 210 | 1013 | 51 | |
| 749 | 749 | 395 | 790 | 954 | 925 | 758 | 477 | 507 | 461 | 1023 | 549 | 747 | 826 | 1014 | 741 | 926 | 463 | 943 | 1093 | 922 | 783 | 1063 | 413 | 805 | 391 | 1098 | 782 | 1083 | 379 | |
| 677 | 677 | 251 | 502 | 905 | 141 | 800 | 1004 | 311 | 50 | 745 | 885 | 282 | 994 | 622 | 200 | 890 | 445 | 387 | 231 | 100 | 774 | 924 | 497 | 707 | 564 | 667 | 25 | 462 | 400 | |
| 584 | 584 | 65 | 130 | 520 | 599 | 27 | 260 | 977 | 760 | 294 | 216 | 95 | 108 | 851 | 834 | 292 | 146 | 588 | 864 | 417 | 73 | 147 | 54 | 1040 | 190 | 432 | 380 | 625 | 565 | |
| 229 | 229 | 458 | 916 | 355 | 165 | 326 | 729 | 317 | 434 | 731 | 402 | 330 | 201 | 634 | 633 | 666 | 333 | 359 | 505 | 868 | 718 | 917 | 652 | 710 | 660 | 804 | 217 | 1010 | 163 | |
| 600 | 600 | 97 | 194 | 776 | 283 | 753 | 388 | 898 | 116 | 846 | 509 | 566 | 806 | 693 | 464 | 300 | 150 | 589 | 933 | 232 | 75 | 423 | 403 | 449 | 29 | 1018 | 58 | 763 | 928 | |
| 422 | 422 | 844 | 585 | 134 | 1041 | 673 | 67 | 536 | 111 | 220 | 972 | 979 | 486 | 1072 | 444 | 211 | 657 | 440 | 579 | 222 | 880 | 110 | 243 | 268 | 855 | 841 | 607 | 55 | 888 | |
| 501 | 501 | 1002 | 901 | 295 | 308 | 535 | 699 | 77 | 516 | 188 | 971 | 616 | 1037 | 154 | 961 | 802 | 401 | 376 | 575 | 1032 | 752 | 94 | 1070 | 590 | 129 | 839 | 258 | 47 | 819 | |
| 620 | 620 | 137 | 274 | 1096 | 991 | 6 | 548 | 1075 | 414 | 433 | 48 | 879 | 24 | 1047 | 553 | 310 | 155 | 866 | 192 | 828 | 629 | 768 | 12 | 1089 | 655 | 96 | 207 | 384 | 3 | |
| 556 | 556 | 9 | 18 | 72 | 49 | 411 | 36 | 288 | 784 | 431 | 1082 | 98 | 541 | 576 | 930 | 278 | 139 | 862 | 1019 | 465 | 621 | 767 | 822 | 144 | 196 | 1061 | 392 | 935 | 757 | |
| 296 | 296 | 592 | 81 | 324 | 772 | 195 | 162 | 193 | 219 | 285 | 457 | 441 | 780 | 386 | 876 | 148 | 74 | 570 | 725 | 438 | 37 | 694 | 390 | 648 | 882 | 914 | 661 | 347 | 649 | |
| 479 | 479 | 958 | 813 | 1046 | 191 | 364 | 523 | 875 | 850 | 532 | 706 | 382 | 353 | 647 | 91 | 791 | 947 | 1064 | 618 | 597 | 1025 | 266 | 728 | 989 | 764 | 309 | 425 | 133 | 182 | |
| **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** |
A quick explanation here on this [ 19 rows x 29 columns ] { Multiplication Table } :
The [ 19 x 29 ] { Multiplication Table } is therefore split into four (4) separate sections :
And we shall take note here of a very important feature for this [ 19 x 29 ] { Multiplication Table } :
Let us now take a closer look at this [ 18 x 28 ] { orange-color } area .
And let us now arbitrarily pick a { number } here and do a { keep on 'squaring' } operation to see if it arrives back at the same { number } :

| 1 | 2 | 4 | 16 | 256 | 459 | 8 | 64 | 787 | 586 | 363 | 512 | 733 | 128 | 942 | 552 | 276 | 69 | 349 | 471 | 138 | 293 | 918 | 32 | 1024 | 726 | 945 | 698 | 781 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 4 | 16 | 256 | 459 | 8 | 64 | 787 | 586 | 363 | 512 | 733 | 128 | 942 | 552 | 276 | 69 | 349 | 471 | 138 | 293 | 918 | 32 | 1024 | 726 | 945 | 698 | 781 | |
| 17 | 17 | 34 | 68 | 272 | 1043 | 82 | 136 | 1088 | 143 | 35 | 656 | 983 | 328 | 1073 | 572 | 560 | 280 | 70 | 418 | 286 | 140 | 569 | 164 | 544 | 863 | 209 | 632 | 836 | 41 | |
| 289 | 289 | 578 | 53 | 212 | 83 | 291 | 106 | 848 | 225 | 595 | 122 | 166 | 61 | 593 | 900 | 696 | 348 | 87 | 488 | 450 | 174 | 849 | 582 | 424 | 332 | 244 | 664 | 976 | 697 | |
| 796 | 796 | 489 | 978 | 603 | 824 | 271 | 853 | 206 | 1051 | 990 | 1065 | 545 | 1084 | 412 | 895 | 398 | 199 | 877 | 951 | 999 | 651 | 495 | 542 | 103 | 1090 | 1027 | 1077 | 799 | 687 | |
| 494 | 494 | 988 | 873 | 183 | 722 | 631 | 643 | 732 | 522 | 498 | 636 | 341 | 318 | 361 | 985 | 247 | 675 | 996 | 338 | 1044 | 889 | 249 | 159 | 366 | 682 | 169 | 261 | 676 | 867 | |
| 273 | 273 | 546 | 1092 | 1059 | 399 | 668 | 1081 | 927 | 869 | 43 | 932 | 798 | 466 | 751 | 167 | 688 | 344 | 86 | 419 | 635 | 172 | 573 | 233 | 1015 | 493 | 761 | 986 | 838 | 334 | |
| 628 | 628 | 153 | 306 | 121 | 833 | 369 | 612 | 484 | 92 | 709 | 746 | 563 | 373 | 968 | 368 | 314 | 157 | 315 | 778 | 184 | 630 | 906 | 738 | 242 | 23 | 389 | 46 | 453 | 736 | |
| 613 | 613 | 123 | 246 | 984 | 302 | 102 | 492 | 627 | 420 | 743 | 816 | 604 | 408 | 151 | 577 | 858 | 429 | 383 | 1058 | 840 | 766 | 923 | 204 | 865 | 105 | 529 | 210 | 1013 | 51 | |
| 749 | 749 | 395 | 790 | 954 | 925 | 758 | 477 | 507 | 461 | 1023 | 549 | 747 | 826 | 1014 | 741 | 926 | 463 | 943 | 1093 | 922 | 783 | 1063 | 413 | 805 | 391 | 1098 | 782 | 1083 | 379 | |
| 677 | 677 | 251 | 502 | 905 | 141 | 800 | 1004 | 311 | 50 | 745 | 885 | 282 | 994 | 622 | 200 | 890 | 445 | 387 | 231 | 100 | 774 | 924 | 497 | 707 | 564 | 667 | 25 | 462 | 400 | |
| 584 | 584 | 65 | 130 | 520 | 599 | 27 | 260 | 977 | 760 | 294 | 216 | 95 | 108 | 851 | 834 | 292 | 146 | 588 | 864 | 417 | 73 | 147 | 54 | 1040 | 190 | 432 | 380 | 625 | 565 | |
| 229 | 229 | 458 | 916 | 355 | 165 | 326 | 729 | 317 | 434 | 731 | 402 | 330 | 201 | 634 | 633 | 666 | 333 | 359 | 505 | 868 | 718 | 917 | 652 | 710 | 660 | 804 | 217 | 1010 | 163 | |
| 600 | 600 | 97 | 194 | 776 | 283 | 753 | 388 | 898 | 116 | 846 | 509 | 566 | 806 | 693 | 464 | 300 | 150 | 589 | 933 | 232 | 75 | 423 | 403 | 449 | 29 | 1018 | 58 | 763 | 928 | |
| 422 | 422 | 844 | 585 | 134 | 1041 | 673 | 67 | 536 | 111 | 220 | 972 | 979 | 486 | 1072 | 444 | 211 | 657 | 440 | 579 | 222 | 880 | 110 | 243 | 268 | 855 | 841 | 607 | 55 | 888 | |
| 501 | 501 | 1002 | 901 | 295 | 308 | 535 | 699 | 77 | 516 | 188 | 971 | 616 | 1037 | 154 | 961 | 802 | 401 | 376 | 575 | 1032 | 752 | 94 | 1070 | 590 | 129 | 839 | 258 | 47 | 819 | |
| 620 | 620 | 137 | 274 | 1096 | 991 | 6 | 548 | 1075 | 414 | 433 | 48 | 879 | 24 | 1047 | 553 | 310 | 155 | 866 | 192 | 828 | 629 | 768 | 12 | 1089 | 655 | 96 | 207 | 384 | 3 | |
| 556 | 556 | 9 | 18 | 72 | 49 | 411 | 36 | 288 | 784 | 431 | 1082 | 98 | 541 | 576 | 930 | 278 | 139 | 862 | 1019 | 465 | 621 | 767 | 822 | 144 | 196 | 1061 | 392 | 935 | 757 | |
| 296 | 296 | 592 | 81 | 324 | 772 | 195 | 162 | 193 | 219 | 285 | 457 | 441 | 780 | 386 | 876 | 148 | 74 | 570 | 725 | 438 | 37 | 694 | 390 | 648 | 882 | 914 | 661 | 347 | 649 | |
| 479 | 479 | 958 | 813 | 1046 | 191 | 364 | 523 | 875 | 850 | 532 | 706 | 382 | 353 | 647 | 91 | 791 | 947 | 1064 | 618 | 597 | 1025 | 266 | 728 | 989 | 764 | 309 | 425 | 133 | 182 | |
| **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** |
And we see here that when we 'square' the number [ 604 mod 1103 ] , we move diagonally 'forward' to the number [ 826 mod 1103 ] .
Let us now try to understand why this is so :

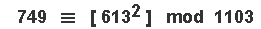
and 'squaring' [ 512 mod 1103 ] will move us one-notch 'forward' on the { RING OF 28 } ,


Thus , 'squaring' any of the 504 { numbers } in this [ 18 x 28 ] { orange-color area } will move us 'forward' in a diagonal direction .
And { keep-on 'squaring' } 28 times will move us , from the original [ 604 mod 1103 ] , to [ 441 mod 1103 ] as marked-off in { white-color } in the { Multiplication Table } above ,
which shall always remain unbroken because both the { RING OF 18 } and the { RING OF 28 } are 'circular' in nature .
Let us now repeat this [ { keep-on-squaring } 28 times ] operation another eight (8) rounds to arrive back at the number [ 604 mod 1103 ] ,
| 1 | 2 | 4 | 16 | 256 | 459 | 8 | 64 | 787 | 586 | 363 | 512 | 733 | 128 | 942 | 552 | 276 | 69 | 349 | 471 | 138 | 293 | 918 | 32 | 1024 | 726 | 945 | 698 | 781 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 4 | 16 | 256 | 459 | 8 | 64 | 787 | 586 | 363 | 512 | 733 | 128 | 942 | 552 | 276 | 69 | 349 | 471 | 138 | 293 | 918 | 32 | 1024 | 726 | 945 | 698 | 781 | |
| 17 | 17 | 34 | 68 | 272 | 1043 | 82 | 136 | 1088 | 143 | 35 | 656 | 983 | 328 | 1073 | 572 | 560 | 280 | 70 | 418 | 286 | 140 | 569 | 164 | 544 | 863 | 209 | 632 | 836 | 41 | |
| 289 | 289 | 578 | 53 | 212 | 83 | 291 | 106 | 848 | 225 | 595 | 122 | 166 | 61 | 593 | 900 | 696 | 348 | 87 | 488 | 450 | 174 | 849 | 582 | 424 | 332 | 244 | 664 | 976 | 697 | |
| 796 | 796 | 489 | 978 | 603 | 824 | 271 | 853 | 206 | 1051 | 990 | 1065 | 545 | 1084 | 412 | 895 | 398 | 199 | 877 | 951 | 999 | 651 | 495 | 542 | 103 | 1090 | 1027 | 1077 | 799 | 687 | |
| 494 | 494 | 988 | 873 | 183 | 722 | 631 | 643 | 732 | 522 | 498 | 636 | 341 | 318 | 361 | 985 | 247 | 675 | 996 | 338 | 1044 | 889 | 249 | 159 | 366 | 682 | 169 | 261 | 676 | 867 | |
| 273 | 273 | 546 | 1092 | 1059 | 399 | 668 | 1081 | 927 | 869 | 43 | 932 | 798 | 466 | 751 | 167 | 688 | 344 | 86 | 419 | 635 | 172 | 573 | 233 | 1015 | 493 | 761 | 986 | 838 | 334 | |
| 628 | 628 | 153 | 306 | 121 | 833 | 369 | 612 | 484 | 92 | 709 | 746 | 563 | 373 | 968 | 368 | 314 | 157 | 315 | 778 | 184 | 630 | 906 | 738 | 242 | 23 | 389 | 46 | 453 | 736 | |
| 613 | 613 | 123 | 246 | 984 | 302 | 102 | 492 | 627 | 420 | 743 | 816 | 604 | 408 | 151 | 577 | 858 | 429 | 383 | 1058 | 840 | 766 | 923 | 204 | 865 | 105 | 529 | 210 | 1013 | 51 | |
| 749 | 749 | 395 | 790 | 954 | 925 | 758 | 477 | 507 | 461 | 1023 | 549 | 747 | 826 | 1014 | 741 | 926 | 463 | 943 | 1093 | 922 | 783 | 1063 | 413 | 805 | 391 | 1098 | 782 | 1083 | 379 | |
| 677 | 677 | 251 | 502 | 905 | 141 | 800 | 1004 | 311 | 50 | 745 | 885 | 282 | 994 | 622 | 200 | 890 | 445 | 387 | 231 | 100 | 774 | 924 | 497 | 707 | 564 | 667 | 25 | 462 | 400 | |
| 584 | 584 | 65 | 130 | 520 | 599 | 27 | 260 | 977 | 760 | 294 | 216 | 95 | 108 | 851 | 834 | 292 | 146 | 588 | 864 | 417 | 73 | 147 | 54 | 1040 | 190 | 432 | 380 | 625 | 565 | |
| 229 | 229 | 458 | 916 | 355 | 165 | 326 | 729 | 317 | 434 | 731 | 402 | 330 | 201 | 634 | 633 | 666 | 333 | 359 | 505 | 868 | 718 | 917 | 652 | 710 | 660 | 804 | 217 | 1010 | 163 | |
| 600 | 600 | 97 | 194 | 776 | 283 | 753 | 388 | 898 | 116 | 846 | 509 | 566 | 806 | 693 | 464 | 300 | 150 | 589 | 933 | 232 | 75 | 423 | 403 | 449 | 29 | 1018 | 58 | 763 | 928 | |
| 422 | 422 | 844 | 585 | 134 | 1041 | 673 | 67 | 536 | 111 | 220 | 972 | 979 | 486 | 1072 | 444 | 211 | 657 | 440 | 579 | 222 | 880 | 110 | 243 | 268 | 855 | 841 | 607 | 55 | 888 | |
| 501 | 501 | 1002 | 901 | 295 | 308 | 535 | 699 | 77 | 516 | 188 | 971 | 616 | 1037 | 154 | 961 | 802 | 401 | 376 | 575 | 1032 | 752 | 94 | 1070 | 590 | 129 | 839 | 258 | 47 | 819 | |
| 620 | 620 | 137 | 274 | 1096 | 991 | 6 | 548 | 1075 | 414 | 433 | 48 | 879 | 24 | 1047 | 553 | 310 | 155 | 866 | 192 | 828 | 629 | 768 | 12 | 1089 | 655 | 96 | 207 | 384 | 3 | |
| 556 | 556 | 9 | 18 | 72 | 49 | 411 | 36 | 288 | 784 | 431 | 1082 | 98 | 541 | 576 | 930 | 278 | 139 | 862 | 1019 | 465 | 621 | 767 | 822 | 144 | 196 | 1061 | 392 | 935 | 757 | |
| 296 | 296 | 592 | 81 | 324 | 772 | 195 | 162 | 193 | 219 | 285 | 457 | 441 | 780 | 386 | 876 | 148 | 74 | 570 | 725 | 438 | 37 | 694 | 390 | 648 | 882 | 914 | 661 | 347 | 649 | |
| 479 | 479 | 958 | 813 | 1046 | 191 | 364 | 523 | 875 | 850 | 532 | 706 | 382 | 353 | 647 | 91 | 791 | 947 | 1064 | 618 | 597 | 1025 | 266 | 728 | 989 | 764 | 309 | 425 | 133 | 182 | |
| **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** | **** |
And a summary for the total { 9-rounds operation } is then as follows :
| Start-off Position | Operation for the current { round } | Ending Position | |
|---|---|---|---|
| Round #1 | 604 mod 1103 | 'squaring' 28 times | 441 mod 1103 |
| Round #2 | 441 mod 1103 | 'squaring' 28 times | 282 mod 1103 |
| Round #3 | 282 mod 1103 | 'squaring' 28 times | 983 mod 1103 |
| Round #4 | 983 mod 1103 | 'squaring' 28 times | 330 mod 1103 |
| Round #5 | 330 mod 1103 | 'squaring' 28 times | 545 mod 1103 |
| Round #6 | 545 mod 1103 | 'squaring' 28 times | 979 mod 1103 |
| Round #7 | 979 mod 1103 | 'squaring' 28 times | 798 mod 1103 |
| Round #8 | 798 mod 1103 | 'squaring' 28 times | 879 mod 1103 |
| Round #9 | 879 mod 1103 | 'squaring' 28 times | 604 mod 1103 |
We can then conclude that :
We then have this set of 2 diagrams , being schematic representations of the 2 { RING's OF 252 } :

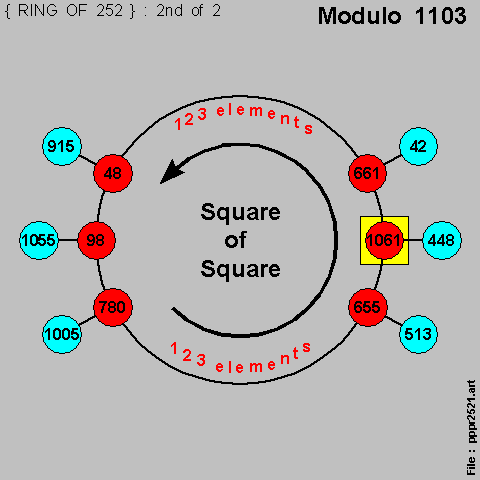
And we note here that the { mutiplicative conjugate pair } [ 604 , 1061 ] are now on 2 separate { RING's } .
But let us also understand why :
This is because :
and these 2 { numbers } are always controlling on the merging of 2 { RING's } .
We have , in this Section , constructed a { Multiplication Table } of { 551 elements } for [ modulo 1103 ] , using the { core elements } :
And we simply note here that the other { 551 elements } , which would then make-up the full field of { 1,102 elements } ,
Thus , the entire field of { 1,102 elements } have been characterized .
Let us now move-on to [ modulo 3361 ] .