Structure of the Multiplication Table for [ modulo P ]

In the Section , we shall construct a { Multiplication Table } for [ modulo 3361 ] ,

• using the { Characteristic Pyramid } & the { Square-Of-Square RING's } ,

  but with a new 'twist' identified here .

The positions of { multiplicative conjugate pairs } are also identified .

For the { prime number } [ P ] being equal to [ 3,361 ] , we set up the corresponding value [ Q ] such that :

• [ Q ] = [ P - 1 ] = [ 3,360 ]

And we can write :

• 3,361 = 32 x 3 x 5 x 7 + 1

We can then set-up the { core elements } for building the { Multiplication Table } for [ modulo 3361 ] , as follows :

• The { Characteristic Pyramid } , based on the { solution set } to the equation :
  • 

• the { RING OF 2 } , based on the { solution set } to the equations :
  • 

    but excluding the solution-value [ 1 ] .

  as per the diagram on-the-left , below .

• the { RING OF 4 } , based on the { solution set } to the equations :
  • 

    but excluding the solution-value [ 1 ] .

  as per the diagram on-the-right , above .

• the { RING OF 6 } , based on the { solution set } to the equation :
  • 

    but excluding the solution-value [ 1 ] ;

  But there is a new 'twist' here :

  • the 6 [ solution values ] to the above equation , other than the solution-value [ 1 ] , forms 2 x { RING's OF 3 } :

• But we can still , nonetheless , arrive at this 'quasi' { RING OF 6 } based on combining the 2 { RING's OF 3 } :



• And the 'squaring-links' shall remain valid , as marked by the 'arrows' .

( This phenomenon of splitting the 'quasi' { RING OF 6 } into 2 x { RING's OF 3 } ] will be further studied in the next Section , on { FIRON - 2/P } . )

Let us now take a quick look at the positions of { multiplicative conjugates } on these { core elements } ,

• before moving-on to the { Multiplication Table } itself , next .

And we bring-in , firstly , the { Characteristic Pyramid } from above :

But we shall now concentrate on the section to-the-right of the { white-color dotted-line } , as marked above ,

• and we present this alternate format for this { sub-section to-the-right } , as follows :

  

  • And the { multiplicative conjugate pairs } here are :
    • [ 1 , 1 ] , as marked-off in { red-color } ; & [ 3360 , 3360 ] , as marked-off in { light-blue-color } ;
    • [ 900, 2461 ] ; as marked-off in { purple-color } ;
    • [ 30 , 3249 ] , [ 3331 , 112 ] ; as marked-off in { green-color };
    • [ 1651 , 3304 ] , [ 1710 , 57 ] , [ 338 , 885 ] , & [ 3023 , 2476 ] ; as marked-off in { yellow-color } .
    • [ 1604 , 2680 ] , [ 1757 , 681 ] , [ 1630 , 2163 ] , [ 1731 , 1198 ] , [ 1066 , 2330 ] , [ 2295 , 1031 ] , [ 1515 , 264 ] , & [ 1846 , 3097 ] ; as marked-off in { white-color } .

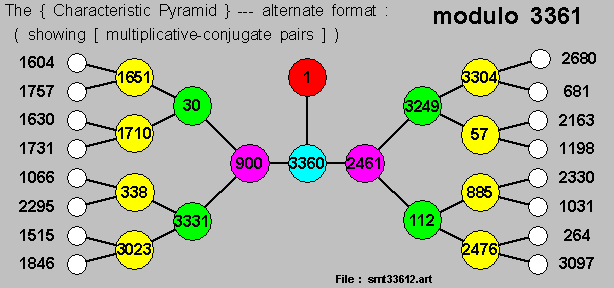
Let us now bring-in the { RING OF 2 } , as per the diagram on-the-left , below :

• and we mark-off several { multiplicative conjugate pairs } here , for indicative purposes :
  • [ 892 , 2468 ] , [ 893 , 2469 ] , [ 2882 , 421 ] , [ 98 , 926 ] , [ 574 , 486 ] , & [ 2775 , 889 ] .

Let us also bring-in the { RING OF 4 } , as per the diagram on-the-right , above :

• and we mark-off several { multiplicative conjugate pairs } here , also for indicative purposes :
  • [ 200 , 2672 ] , [ 2541 , 332 ] , [ 1685 , 1494 ] , [ 123 , 2268 ] , [ 822 , 2302 ] , & [ 1129 , 905 ] .

And finally , we bring-in the 'quasi' { RING OF 6 } :

• and we mark-off several { multiplicative conjugate pairs } here , again for indicative purposes :
  • [ 844 , 2465 ] , [ 1916 , 735 ] , [ 1733 , 3297 ] , [ 1793 , 2883 ] , [ 2746 , 1563 ] , & [ 1550 , 2730 ] .

  

Clearly , { multiplicative conjugate pairs } can be readily & easily identified on the { core elements } , based on their positions in each of the structures ;

• with { multiplicative conjugate pairs } resident on the { outer-portion } of the { RING's } being directly derivable from :
  • the positions of the { multiplicative conjugate pairs } on the { Characteristic Pyramid } , &

  • the positions of the { multiplicative conjugate pairs } on the { core / inner portion } of the { RING's } .

We then have this 3-Dimension [ 3 x 5 x 7 ] { Multiplication Table } for [ modulo 3361 ] with :

• the range of 'X' being { 1 , 892 , 2468 } ,
• the range of 'Y' being { 1 , 200 , 3029 , 2672 , 820 } , &
• the range of 'Z' being { 1 , 844 , 3165 , 1445 , 2465 , 2898 , 2626 } .

  and we have this { 3-layers presentation } of the { Multiplication Table } as follows :

  

  

  

  • the { white-color dotted-line } in each of diagrams is then a simple reminder that the 'quasi' { RING OF 6 } is in fact made-up-of 2 x [ RING's OF 3 ] , with :
    • { 844 - 3165 - 1445 } [ modulo 3361 ] being one set of closed-loop { squaring relations } , &

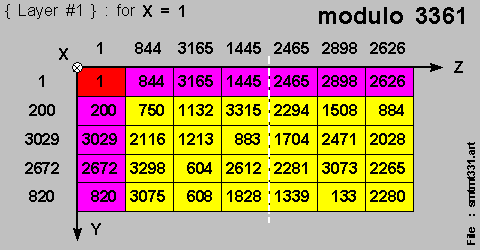
      { 2465 - 2898 - 2626 } [ modulo 3361 ] being another set of closed-loop { squaring relations } ;

      • separate from one-another ,

    so that { crossing-over the white-color dotted-line } is not allowed .

Let us now take a look at each of the differently-colored area in the { Multiplication Table } above :

• the { red-color area } is simply the single cell for [ 1 x 1 x 1 ] [ modulo 3361 ] ;

• the { pinkish-purple-color area } then identifies the locations for :
  • [ 1 ] x [ RING OF 2 ] ,
  • [ 1 ] x [ RING OF 4 ] , &
  • [ 1 ] x 'quasi' [ RING OF 6 ] ;

• the { yellow-color area } then identifies where :
  • the [ RING OF 4 ] & the 'quasi' [ RING OF 6 ] merge ,
  • the [ RING OF 2 ] & the 'quasi' [ RING OF 6 ] merge , &
  • the [ RING OF 2 ] & the [ RING OF 4 ] merge .

• the { light-green-color area } then identifies where all 3 [ RING's ] merge together ,
  • and therefore has [ 2 x 4 x 6 ] or 48 elements .

Let us now take a look at the 4 x { RING's OF 12 } for the 48 elements in the { light-green-color area } :

• And we have marked-off the { multiplicative conjugate pairs } :
  • [ 161 , 3194 ] & [ 1951 , 789 ] for indicative purposes .

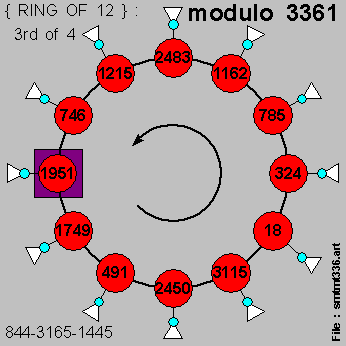
  And we also note here that :

  • the 2 x { RING's OF 12 } on-the-left arise from the [ 844-3165-1445 ] { RING OF 3 } , &

  • the 2 x { RING's OF 12 } on-the-right arise from the [ 2465-2898-2626] { RING OF 3 } ;

    so that each of the 2 { multiplicative conjugate pairs } indicated above are also on { separate RING's } .

But let us also understand why there are 4 x { RING's OF 12 } here .

This is because :

• when we merge the { RING OF 2 } with the { RING OF 4 } , we get 2 x { RING's OF 4 } ,
  • arising from :
    • { G.C.D. ( 2 , 4 ) } = 2 ,
    • { L.C.M. ( 2 , 4 ) } = 4 .

• when we merge one of these derived { RING's OF 4 } with either of the 2 { RING's OF 3 } , we get a new { RING OF 12 } ,
  • arising from :
    • { G.C.D. ( 4 , 3 ) } = 1 ,
    • { L.C.M. ( 4 , 3 ) } = 12 .

  so that there are now [ 2 x 2 ] or 4 x { RING's OF 12 } .

We have , in this Section , constructed a { Multiplication Table } of { 105 elements } for [ modulo 3361 ] , using the { core elements } :

• the { Characteristic Pyramid } , the { RING OF 2 } , the { RING OF 4 } , & the 'quasi' { RING OF 6 } .

And we simply note here that :

• there are always another { 31 associated elements } attached to each of these { 105 elements } ,
  • with the attachments being based on the { Characteristic Pyramid } and/or its derived { pyramids } ,

  so that the full field of [ 32 x 105 ] or { 3360 elements } has now been fully characterized .

And we are now ready to move-on to next Section , on why the size of the { RING's } are controlled by { FIRON - 2/P } .