Structure of the Multiplication Table for [ modulo P ]

In this Section , we shall bring-in again the { Square-Of-Square } concept for [ modulo P ] ,

For any 'odd' { prime number } , [ P ] , greater than [ 3 ] , we always set-up the value [ Q ] such that :

• [ Q ] = [ P - 1 ]

And we simply note here that [ Q ] is an important quantity arising from the { Fermat Little Theorem } .

Let us now go thru the basic mechanics for the { Square-Of-Square Process } , as folllows :

• STEP I :

  We first set-up an initial { set } , { Set Zero } , consisting of 'Q' members :

  • with each member being a { positive integer } ranging from [ 1 ] to [ Q ] .

• STEP II :

  We then 'square' each and every member of { Set Zero } and take the [ modulo P ] value thereof to form a new { set } , { Set #1 } :

  • with { Set #1 } having a reduced { number of members } .

• STEP III :

  We then 'square' each and every member of { Set #1 } and take the [ modulo P ] value thereof to form a new { set } , { Set #2 } :

  • with { Set #2 } either :
    • having a reduced { number of members } ,

    or :

    • having the same { number of members } as { Set #1 } .

  If { Set #2 } have the same { number of members } as { Set #1 } ,

  • the { Square-Of-Square Process } stops here ;

  otherwise , we continue & repeat the { squaring process } until :

  • the { number of members } in the newly-formed { set } can no longer be reduced , any further .

This very-last { set } , and the { set } immediately-previous to it , would then have the same { number of members } .

We shall see at a later stage that these two (2) { sets } are in fact identical , so that :

• either of these can be used / labelled as the { Core Square-Of-Square Set } for [ modulo P ] .

Let us now take a quick look at an example , for the { prime number } [ 41 ] :

• We then set-up the value [ Q ] , i.e. :
  • [ Q ] = [ P - 1 ] = 40

We then set-up the initial { set } , { Set Zero } , consisting of 40 members ranging from [ 1 ] to [ Q ] , i.e. :

• { Set Zero } = { 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15 , 16 , 17 , 18 , 19 , 20 , 21 , 22 , 23 , 24 , 25 , 26 , 27 , 28 , 29 , 30 , 31 , 32 , 33 , 34 , 35 , 36 , 37 , 38 , 39 , 40 }

We then 'square' each & every member of { Set Zero } , and take the value [ modulo 41 ] thereof , as per this table below :

• to arrive { Set #1 } , a reduced { set } consisting of only { 20 members } , as follows :
  • { Set #1 } = { 1 , 2 , 4 , 5 , 8 , 9 , 10 , 16 , 18 , 20 , 21 , 23 , 25 , 31 , 32 , 33 , 36 , 37 , 39 , 40 }

We then 'square' each & every member of { Set #1 } , and take the value [ modulo 41 ] thereof , as per this table below :

• to arrive at { Set #2 } , a reduced { set } consisting of only { 10 members } , as follows :
  • { Set #2 } = { 1 , 4 , 10 , 16 , 18 , 23 , 25 , 31 , 37 , 40 }

We then 'square' each & every member of { Set #2 } , and take the value [ modulo 41 ] thereof , as per this table below :

• to arrive at { Set #3 } , a reduced { set } consisting of only { 5 members } , as follows :
  • { Set #3 } = { 1 , 10 , 16 , 18 , 37 }

We then 'square' each & every member of { Set #3 } , and take the value [ modulo 41 ] thereof , as per this table below :

• to arrive at { Set #4 } , a { set } consisting of { 5 members } , as follows :
  • { Set #4 } = { 1 , 10 , 16 , 18 , 37 }

  But there are no further reductions in the { number of members } here .

And { Set #3 } , with { 5 members } and identical to { Set #4 } , is then our final { Core Square-Of-Square Set } for [ modulo 41 ] .

Two (2) key observations here :

• the { number } [ 1 ] is always a member of each & every { set } ; because :
  • 

• there are four ( 4 ) members other than the { number } [ 1 ] in the final { Core Square-Of-Square Set } , i.e. :
  • the { numbers } [ 10 ] , [ 16 ] , [ 18 ] , & [ 37 ] ;

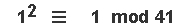
    and these 4 { numbers } then form a { RING } of { squaring relations } , i.e. :

    • 

      

      

      

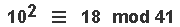
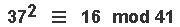
Let us now take a close look at several key observations , on { Square-Of-Square } , next .

The 1st key observation here is this :

• If [ X ] & [ Y ] is a pair of { additive conjugates } , [ modulo P ] ,

  then they share the same value [ Z ] as the value of their squares .

Let us start-off with the case where two (2) { numbers } , [ X ] & [ Y ] , shares that same value [ Z ] as their { squares } , i.e. :

Re-arranging terms then yields :

And consequently :

so that :

• either :
  • 

  or :

  • 

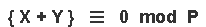
  or both .

Thus , [ Y ] is always the { additive conjugate } of [ X ] , [ modulo P ] , if [ Y ] is not itself congruent to [ X mod P ] .

We then have this diagram on-the-left , below , showing this type of { squaring relations } , where :

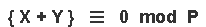
In particular , we also have a specific set of { squaring relations } involving [ 1 ] & [ Q ] , as per the diagram on-the-right , above , i.e. :

The 2nd key observation here is this :

• The { number of elements } in { Set #1 } is always equal to { one-half x [ Q ] } .

This is because :

• We always start with 'Q' elements in { Set Zero } , i.e. : all the { numbers } from [ 1 ] to [ Q ] , so that :
  • there are always { one-half x [ Q ] } distinct pairs of { additive conjugates } here ;

• On 'squaring' each pair of { additive conjugates } , we always :
  • get a [ 1 ] for the { additive conjugate pair } of { 1 , Q } ,

  • get a { number } other than [ 1 ] for all the other { additive conjugate pairs } ,
    • with each of these 'new elements' being different & distinct ,

      because each pair of { additive conjugates } cannot share , with another pair of { additive conjugates } ,
      the exact-same { number } as their squares ,

      • unless the two (2) pairs of { additive conjugates } are one-and-the-same pair ;

  so that there are always exactly { one-half x [ Q ] } new elements formed , for { Set #1 } .

The 3rd key observation here is this :

• Any { higher-ordered set } is always a { sub-set } of all { lower-ordered sets } .

And that is to say :

• { Set #1 } is always a { sub-set } of { Set Zero } ,
• { Set #2 } is always a { sub-set } of { Set #1 } ,
• { Set #3 } , if it exists , is always a { sub-set } of { Set #2 } ,
• and so-on-and-so-forth .

Let us start-off the explanation here with this set of diagrams below :

• where :
  • [ Z ] is the square of [ X ] & [ Y ] , [ modulo P ] , &
  • [ A ] is the square of [ Z ] , [ modulo P ] .

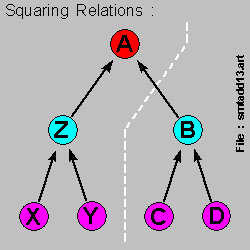
We note here that [ A ] is then the { 4th-power } of [ X ] & [ Y ] , [ modulo P ] .

We can then make these 'rather intuitive' statements as follows :

• the { 4th-power } of [ X ] is also the { square } of a { number } , [ modulo P ] ;

• the { 8th-power } of [ X ] is also the { 4th-power } of a { number } , [ modulo P ] ;

• the { 16th-power } of [ X ] is also the { 8th-power } of a { number } , [ modulo P ] ;

• and so-on-and-so-forth .

It then follows that :

• any member of a { higher-order set } is always a member of the { next-lower-ordered set } ,

  so that :

  • memberships are always successively 'restricted/tightened' as we move along to a { higher-ordered set } ,

    until the { Core Square-Of-Square Set } is reached ,

    • where there can be no further reductions in the { number of members } .

There are two (2) more key observations here , namely , that :

• the { number of members } for each subsequent { set } are always 'halfed' until we reach the { Core Square-Of-Square Set } ,

• the { number of members } for the final { Core Square-Of-Square Set } is always an { 'odd' number } ;
  • with the number [ 1 ] always standing alone-by-itself , &

  • with the remaining 'even-number' of members being { multiplicative conjugate pairs } ,
    • forming one or more [ RING's ] of 'squaring relations' .

The mechanics of both are clearly demonstrated in the next Section --- Topic #5 ,

• when we attach { sub-pyramid-extensions to the [ RING's ] } .

But we are still baffled at this point on 2006-6-25 as to the best way of closing-in on the proof / derivation ,

• although { FIRON - 2/P } in Section VI could possibly help .

We shall put the proof in Appendix B at a later stage when the same is available . Our apologies here .