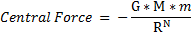An Approach to Mathematic Functions Basics

by Frank C. Fung ( 1st published in December, 2014. )

Top Of Page

Section XXX - The Case of the Circular Orbit as the Base Scenario

Summary for the Section :

• In this Section , we shall take a close look :
  • at the mechanics of a Satellite moving in a Circular Orbit .

  And we shall also briefly explain as to why it is important that :

  • we must select the case of the Circular Orbit as the Base Scenario .

go to Top Of Page

The Key Feature of the Circular Orbit :

• The key feature of the Circular Orbit is simply that :
  • the Satellite is always travelling in a circle centered at the Point-Of-Origin ,
    • with the Point-Of-Origin here being the fixed-point where the Central Force originates .

  

  Let us identify , at this point , these four (4) key quantities below :

  • 

  • 

  • 

  • 
    

    which together will fully define the characteristics of the Circular Orbit .

  ( The [ CIRO ] sub-notation here is then the abbreviation for CIRcular Orbit ) .

• And we shall spell-out in finer details below :
  • as to how these 4 quantities must inter-act with one-another in order that :
    • the Circular Orbit may be formulated properly .

go to Top Of Page

[ R ] for the Circular orbit is constant :

• Let us recall that the key feature of the Circular Orbit is that :
  • the Satellite is always at the same distance away from the Point-Of-Origin .

  Consequently , [ R ] is constant throughout ,

  • and therefore :
    • 

• We shall now set up :
  • 

    where :

    • 

go to Top Of Page

The Velocity for the Circular Orbit is constant :

• Let us recall that , for a Satellite moving under a Central Force :
  • we have already established in Section XXVI that :
    • 

  And since [ R ] is constant throughout for the Circular Orbit ,

  • i.e. :
    • 

    it then follows immediately that :

    • 

• Let us recall that we have previously defined in Section XXVII :
  • 

  • 

  And we have also established in that Section that :

  • 

  • 

  Consequently , for the Satellite travelling in the Circular Orbit , we have :

  • FIRST :
    • 

      arising from :

      • 

  • SECOND :
    • 

      arising from :

      • 

        [ R ] being constant throughout for the Circular Orbit .

      and

      • 

        as established above .

  This then tells us that :

  • the velocity is constant throughout and is always in the [ e-sub-Theta ] direction .

• And based on this , we shall now set up :
  • 

    where :

    • 

go to Top Of Page

Necessary Conditions for the Circular Orbit :

• Let us now take a quick look at the Force Equilibrium of the Satellite moving in the Circular Orbit .

  From elementary Vector Mechanics ,

  • we have this equation for the Centripetal Force acting on the Satellite :
    • 

  And the Central Force acting on the Satellite is given by :

  • 

    being the Gravitational Force varying as the { inverse of [ R-Square ] } .

  Equating the two (2) forces immediately above then yield us this equation :

  • 

  Consequently , we have :

  • 

• And the final equation here is then :
  • 

  And this then is the governing equation for the Circular Orbit ,

  • when the Central Force is a Gravitational Force varying as the { inverse of [ R-Square ] } .

go to Top Of Page

Explaining the Choice of the Circular Orbit as the Base Scenario :

• Let us now take a quick look as to whether or not :
  • the Circular Orbit is also in the repertoire of possible orbits
    • when the Central Force varies as the { inverse of [ R-Cube ] } ;
      • as opposed to :
        • the Central Force varying as the { inverse of [ R-Square ] } above .

  For this particular situation ,

  • the equation for the Centripetal Force would remain unchanged :
    • 

  and

  • the new equation for the Central Force would become :
    • 

  And on equating the two (2) forces , we have :

  • 

    yielding :

  • 

  And the final governing equation here for the Circular Orbit is then :

  • 

    when the Central Force is a Gravitational Force varying as the { inverse of [ R-Cube ] } .

• In general ,
  • when the Central Force is a Gravitational Force varying as the { inverse of [ R-rasied-to-the-Power-N ] } :
    • i.e. :
      • 

    the final governing equation for the Circular Orbit would become :

    • 

• The KEY POINT we are making here is this :
  • For any Centarl Force being a gravitation-type force of the format :
    • 

      with [ N ] being greater than or equal to [ 2 ] ;

    the Circular Orbit is always in the repetorie of possible orbits .

go to Top Of Page

go to the next section : Section XXXI - The Case of the Central Force disappearing totally

go to the last section : Section XXIX - Setting up the Standarized Set of Initial Conditions

return to the MATH Functions Basics HomePage

Original dated 2014-12-07