Structure of the Multiplication Table for [ modulo P ]

In this Section , we start-off with an application of the { multiplicative conjugates } to the { Chinese Remainder Theorem } in Chinese , but later moved onto :

• Fractions Equations ,
• Vector Mechanics ,
• the { DOT Product } .

Interesting 'twists' .

This version of the { Chinese Remainder Theorem } is from { SUNZI's Book of Arithmetics } , ( sunzi suanjing ) , circa around { 0 - 500 A.D. } :

Rough translation is as follows :

• PROBLEM :

  Now have 'thing' , but do not know its { number } :

  • divided by [ 3 ] , remainder is [ 2 ] ;
  • divided by [ 5 ] , remainder is [ 3 ] ;
  • divided by [ 7 ] , remainder is [ 2 ] ;

  What is the { number } ?

• ANSWER : The { number } is [ 23 ] .

• ARITHMETICS :
  • { divided by [ 3 ] , remainder is [ 2 ] } , place [ 140 ] ;
  • { divided by [ 5 ] , remainder is [ 3 ] } , place [ 63 ] ;
  • { divided by [ 7 ] , remainder is [ 2 ] } , place [ 30 ] ;

  Sum up { Total Placement } , get [ 233 ] .

  Subtract by [ 210 ] , get [ 23 ] .

  Whenever :

  • { divided by [ 3 ] , remainder is [ 1 ] } , place [ 70 ] ;
  • { divided by [ 5 ] , remainder is [ 1 ] } , place [ 21 ] ;
  • { divided by [ 7 ] , remainder is [ 1 ] } , place [ 15 ] ;

  Whenever { Total Placement } is [ 106 ] & over , subtract [ 105 ] & get it .

Here is then a follow-up on the { arithmetic calculation procedure } , explained via { modern-day } mathematics .

For the numbers [ 3 ] , [ 5 ] , & [ 7 ] being { relatively prime } numbers ,

• we shall first try to find a value [ W ] satisfying the equations :
  • 
  • 
  • 

    with :

    • the range of [ X ] being { 0 , 1 , 2 } ;
    • the range of [ Y ] being { 0 , 1 , 2 , 3 , 4 } ;
    • the range of [ Z ] being { 0 , 1 , 2 , 3 , 4 , 5 , 6 } .

To facilitate our discussions below , let us now set up the values [ M1 ] , [ M2 ] & [ M3 ] , being the { prime modulo's } , as follows :

• [ M1 ] = 3 ,
• [ M2 ] = 5 ,
• [ M3 ] = 7 .

We can now do our search for the value of [ W ] :

• We first start-off with calculating the values for the { L.C.M. } and the constants [ K1 ] , [ K2 ] , & [ K3 ] , as follows :
  • { L.C.M. } = 3 x 5 x 7 = [ 105 ] ,

    i.e. :

    • { L.C.M. } = [ M1 ] * [ M2 ] * [ M3 ] ;

  • for the constants [ K's ] :
    • [ K1 ] = 5 x 7 = [ 35 ] ,
    • [ K2 ] = 7 x 3 = [ 21 ] ,
    • [ K3 ] = 3 x 5 = [ 15 ] ;

      i.e. :

      • [ K1 ] = [ M2 ] * [ M3 ] ,
      • [ K2 ] = [ M3 ] * [ M1 ] ,
      • [ K3 ] = [ M1 ] * [ M2 ] ;

      or alternately :

      • [ K1 ] = { L.C.M. } / [ M1 ] ,
      • [ K2 ] = { L.C.M. } / [ M2 ] ,
      • [ K3 ] = { L.C.M. } / [ M3 ] .

• We then try to find the values of the { co-efficients } , [ C1 ] , [ C2 ] & [ C3 ] respectively , satisfying the relations :
  • ,
  • ,
  • .

  And the solutions to these 3 equations are :

  • ,
  • ,
  • ;

    yielding :

    • the value of [ C1 ] being equal to [ 2 ] ,
    • the value of [ C2 ] being equal to [ 1 ] ,
    • the value of [ C3 ] being equal to [ 1 ] .

• The general formula for the value of [ W ] , expressed in terms of [ X ] , [ Y ] & [ Z ] , is then :
  • 

    This is because :

    • the value { [ C1 ] * [ K1 ] } is always congruent to { [ 1 ] mod [ M1 ] } , { [ 0 ] mod [ M2 ] } , & { [ 0 ] mod [ M3 ] } ;
    • the value { [ C2 ] * [ K2 ] } is always congruent to { [ 0 ] mod [ M1 ] } , { [ 1 ] mod [ M2 ] } , & { [ 0 ] mod [ M3 ] } ;
    • the value { [ C3 ] * [ K3 ] } is always congruent to { [ 0 ] mod [ M1 ] } , { [ 0 ] mod [ M2 ] } , & { [ 1 ] mod [ M3 ] } ;

      so that the value of [ W ] , thus expressed above , is necessarily :

      • congruent to { [ X ] mod [ M1 ] } ,
      • congruent to { [ Y ] mod [ M2 ] } ,
      • congruent to { [ Z ] mod [ M3 ] } .

• We can then set up the anchoring value [ w ] , given by :
  • 

    so that all other alternate values of [ W ] satisfying the original set of 3 equations above , would be governed by the condition :

    • ,

      with [ N ] being any { positive integer } .

Let us now plug-in the values for the [ C's ] & the [ K's ] to arrive at this equation for the value [ W ] :

• [ W ] = { 2 * 35 * X } + { 1 * 21 * Y } + { 1 * 15 * Z }

yielding ,

• [ W ] = { 70 * X } + { 21 * Y } + { 15 * Z }

And plugging in the { remainders } from the orginal problem , i.e. the values of { X = 2 , Y = 3 , Z = 2 } , we then have :

• [ W ] = 70 x [ 2 ] + 21 x [ 3 ] + 15 x [ 2 ] = [ 233 ] ,

  as expected .

Let us now take a look at the values of [ W ] , for the different values of :

• [ X ] being { 0 , 1 , 2 } ,
• [ Y ] being { 0 , 1 , 2 , 3 , 4 } ,
• [ Z ] being { 0 , 1 , 2 , 3 , 4 , 5 , 6 } ;

  as per the set of 3 diagrams on-the-left , below .

And we also present the corresponding values of [ w's ] , [ modulo 105 ] ,

• as per the set of 3 diagrams on-the-right , below .

• And each set of 3 diagrams then forms a { 3 x 5 x 7 Box } , which we shall further make-use-of , later in { Topic #8 } below .

For the set of 3 diagrams on-the-left , we have marked-off :

• the cell for [ W = 0 ] , in { red color } ,

• the cells with [ W ] ranging from [ 1 ] to [ 105 ] , in { light-blue color } ,

• the cells with [ W ] ranging from [ 106 ] to [ 210 ] , in { white color } ,

• the cells with [ W ] ranging from [ 211 ] to [ 315 ] , in { true-blue color } ,

For the set of 3 diagrams on-the-right, we have marked-off :

• in { red color } , the cell for { 0 , 0 , 0 } with [ W = 0 ] ;

• in { pink-purple color } , the cells for :
  • { X , 0 , 0 } , with [ X ] being non-zero ;
  • { 0 , Y , 0 } , with [ Y ] being non-zero ;
  • { 0 , 0 , Z } , with [ Z ] being non-zero .

• in { yellow color } , the cells for :
  • { 0 , Y , Z } , with [ Y ] & [ Z ] being non-zero's ;
  • { X , 0 , Z } , with [ Z ] & [ X ] being non-zero's ;
  • { X , Y , 0 } , with [ X ] & [ Y ] being non-zero's .

• in { green color } , the cells for :
  • { X , Y , Z } , with [ X ] , [ Y ] & [ Z ] being non-zero's .

And we take note here that all the [ w's ] in the { green-color } region are always not divisible by [ 3 ] , [ 5 ] & [ 7 ] ,

• because the remainders [ X ] , [ Y ] & [ Z ] are all non-zero's in this region .

Furthermore , each and every { 'odd' prime number less than [ 105 ] } , other than [ 3 ] , [ 5 ] & [ 7 ] ,

• are identified in this { green color } region ;

  and we present this set of 2 diagrams below for { green color } region , but now marked in { white-color / true-blue color } , to illustrate several points :

• the { white color } region then identifies where the original [ W's ] are in the range of [ 106 ] to [ 210 ] , &
• the { true-blue color } region then identifies where the original [ W's ] are in the range of [ 211 ] to [ 315 ] .

This then illustrates an issue on { parity } , namely :

• for the [ W ] being in the range of [ 106 ] to [ 210 ] :
  • [ w ] is 'odd' whenever [ W ] is 'even' ; &
  • [ w ] is 'even' whenever [ W ] is 'odd' .

• for the [ W ] being in the range of [ 211 ] to [ 315 ] :
  • [ w ] is 'odd' whenever [ W ] is 'odd' ; &
  • [ w ] is 'even' whenever [ W ] is 'even' .

  And this issue on { parity } will be further discussed in { Topic #7 } , below .

And the very special phenomenon of { all 'primes' being identified } , above , then arises because the { square-root } of [ 105 ] is roughly [ 10.25 ] , and

• the only { 'odd' prime numbers less than [ 10.25 ] } are then [ 3 ] , [ 5 ] , & [ 7 ] respectively ,

  so that :

  • all non-prime { 'odd' numbers less than [ 105 ] } are always divisible by [ 3 ] , [ 5 ] , and/or [ 7 ] ;

  • all prime { 'odd' numbers less than [ 105 ] } other than [ 3 ] , [ 5 ] & [ 7 ] are :
    • always { relatively prime } with respect to [ 3 ] , [ 5 ] & [ 7 ] ,

      and this is already a sufficient & governing condition here for the { 'odd' prime numbers less than [ 105 ] } being 'prime' .

Let us now take a look at an application of the { Chinese Remainder Theorem } ,

• to the first ten (10) { 'odd' prime numbers } other than [ 1 ] , i.e :

  the 'prime' numbers : { 3 , 5, 7 , 11 , 13 , 17 , 19 , 23 , 29 , 31 } .

We then set up the values for the { M's } , the { prime modulo's } , as follows :

• [ M1 ] = 3 ,
• [ M2 ] = 5 ,
• [ M3 ] = 7 ,
• [ M4 ] = 11 ,
• [ M5 ] = 13 ,
• [ M6 ] = 17 ,
• [ M7 ] = 19 ,
• [ M8 ] = 23 ,
• [ M9 ] = 29 ,
• [ M10 ] = 31 .

And we also set-up 9 { L.C.M.'s } , correspondingly , as follows :

• [ 15 ] = 3 x 5 ,
• [ 105 ] = 3 x 5 x 7 ,
• [ 1155 ] = 3 x 5 x 7 x 11 ,
• [ 1 5015 ] = 3 x 5 x 7 x 11 x 13 ,
• [ 25 5255 ] = 3 x 5 x 7 x 11 x 13 x 17 ,
• [ 484 9845 ] = 3 x 5 x 7 x 11 x 13 x 17 x 19 ,
• [ 1 1154 6435 ] = 3 x 5 x 7 x 11 x 13 x 17 x 19 x 23 ,
• [ 32 3484 6615 ] = 3 x 5 x 7 x 11 x 13 x 17 x 19 x 23 x 29 ,
• [ 1002 8024 5065 ] = 3 x 5 x 7 x 11 x 13 x 17 x 19 x 23 x 29 x 31 .

We then set up the value [ N ] , being the { number of [ prime modulo's ] } involved with each of the 9 { L.C.M. } , so that we can write :

• ,

  with [ N ] being in the range of [ 2 ] to [ 10 ] here for the 9 { L.C.M.'s } .

We then have this table below for the values of the { constants } [ K's ] :

• 

  for each of the 9 values for the { L.C.M.'s } .

We then set-up the interim values for the [ B's ] , with the [ B's ] being given by :

And we have this table below for the values of the [ B's ] , as follows :

We then have this table below for the values of the { co-efficients } [ C's ] , with the [ C's ] satisfying this relation below :

or its alternate format :

And we simply note here the importance of { multiplicative conjugates } , as applied here .

For each of the 9 { L.C.M.'s } above , let us now try to find the value for [ W ] satisfying the condition :

• 

  with :

  • the range of [ Ri ] being from [ 0 ] to [ Mi - 1 ] ;

  • the value of [ i ] varying from [ 1 ] to [ N ] ,
    • [ N ] being the { number of [ prime modulo's ] } involved with the current { L.C.M. } selected at-hand .

We then set up this formula for the value of [ W ] , as follows :

• 

  based on our discussions in { Topic #3 } above , with :

  • all the values for the { constants [ K's ] } and the { co-efficients [ C's ] } being derivable ,
    • independent(of the values of the [ R's ] ;

    as per our discussions in { Topic #5 } immediately above .

Let us now look at a special case where we have :

and the value of [ W ] is then given by :

• [ W ] = [ L ] * { L.C.M. } + 1 ,
  • where [ L ] is either a { positive integer } or the value [ 0 ] ;

  so that :

  • the { remainders [ R's ] } ,
    • when [ W ] is divided by the value [ Mi ] ,

    are always all equal to [ 1 ] .

  ( This is because [ Mi ] is always divisible into { [ L ] * { L.C.M. } } , by definition of { L.C.M. } . )

Conversely , if the selected values for all the [ R's ] in the 'initial-condition' equations :

• ,

  are all equal to [ 1 ] ;

then the value of [ W ] given by :

• [ W ] = [ L ] * { L.C.M. } + 1

  will always satisfy these conditions .

Let us now bring back this general formula for [ W ] from above :

With all the [ R's ] being equal to [ 1 ] , we then have :

Plugging-in the formula for the { constants [ K's ] } then yields :

Re-arranging terms then yields :

Pluggin-in the value { [ W ] = [ L ] * { L.C.M. } + 1 } then gives us this equation :

Dividing throughout by { L.C.M. } , we then have :

Let us now look at the empirical values for this equation , for each of the 9 { L.C.M.'s } above :

• For { N = 2 } & the { L.C.M. } being [ 15 ] :

  

• For { N = 3 } & the { L.C.M. } being [ 105 ] :

  

• For { N = 4 } & the { L.C.M. } being [ 1155 ] :

  

• For { N = 5 } & the { L.C.M. } being [ 1 5015 ] :

  

• For the { L.C.M. } being [ 25 5255 ] :

  

• For { N = 7 } & the { L.C.M. } being [ 484 9845 ] :

  

• For { N = 8 } & the { L.C.M. } being [ 1 1154 6435 ] :

  

• For { N = 9 } & the { L.C.M. } being [ 32 3484 6615 ] :

  

• For { N = 10 } & the { L.C.M. } being [ 1002 8024 5065 ] :

  

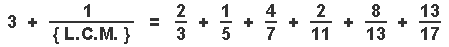
Interesting , eh !

And this then set the stage for us to move-on to { Vector Mechanics } for { numbers } , next .

Let us now bring back the { 3 x 5 x 7 } Box for [ modulo 105 ] , from { Topic #4 } above , with the 3 layers as shown below :

Let us now set-up a { 3-Dimensional Vector Space } , and let us :

• draw-up a { 105 x 105 x 105 } cube ;

• place the { 3 x 5 x 7 Box } for [ modulo 105 ] we have from { Topic #4 } above , so that :
  • the corner of Box , where the { [ 0 ] cell } resides , just-touching the { Point Of Origin } , [ POINT O ] ,

  as per the diagram on-the-left , below .

Let us now multi-stack identical { 3 x 5 x 7 Boxes } in all 3 { axial-directions } , so that :

• the entire { 105 x 105 x 105 } cubic-space is totally filled-up , and :
  • there are now 35 { stacking levels } in the { X-direction } ,
  • there are now 21 { stacking levels } in the { Y-direction } , &
  • there are now 15 { stacking levels } in the { Z-direction } ;

  as per the diagram on-the-right , above .

There are then [ 35 x 21 x 15 ] , or [ 11,025 ] Boxes within the { 105 x 105 x 105 } cubic-space .

Let us now identify the location of each individual Box via a set of 3 variables , i.e. [ LX ] , [ LY ] , & [ LZ ] respectively , so that :

• [ LX ] identifies the 'Stacking Level' in the { X-Direction } ,
  • with [ LX ] varying from [ 0 ] to [ 34 ] ;

• [ LY ] identifies the 'Stacking Level' in the { Y-Direction } ,
  • with [ LY ] varing from [ 0 ] to [ 20 ] ;

• [ LZ ] identifies the 'Stacking Level' in the { Z-Direction } ,
  • with [ LZ ] varing from [ 0 ] to [ 14 ] .

Let us now also draw-in a general { Position Vector } [ RHO ] , passing thru the point [ POINT P ] ,

• with the co-ordinates of [ POINT P ] being ( 105 , 105 , 105 ) ;

  as per the diagram on-the-left , below .

We notice here that the line { LINE O-P } passes thru many { 3 x 5 x 7 Boxes } , and let us now pick one of these { Boxes } for our further analysis below .

And we shall pick the { Box } at { [ LX ] = 22 , [ LY ] = 13 , [ LZ ] = 9 } :

• as per the diagram on-the-right , above ;

  for our discussion purposes here .

And we were able to ascertain that the line { LINE O-P } passes thru this { BOX } at these locations :

• ( 66 , 66 , 66 ) , ( 67 , 67 , 67 ) , & ( 68 , 68 , 68 ) ; global co-ordiantes basis .

And the localized locations within the { 3 x 5 x 7 } Box are then as shown in the set of 3 diagrams below :

We can then write these equations :

• For the { w = 66 } cell , marked-off in { dark-grey color } above , we have :
  • [ 66 ] = 22 * [ 3 ] + [ 0 ] ,
  • [ 66 ] = 13 * [ 5 ] + [ 1 ] ,
  • [ 66 ] = 9 * [ 7 ] + [ 3 ] ;

• For the { w = 67 } cell , marked-off in { dark-grey color } above , we have :
  • [ 67 ] = 22 * [ 3 ] + [ 1 ] ,
  • [ 67 ] = 13 * [ 5 ] + [ 2 ] ,
  • [ 67 ] = 9 * [ 7 ] + [ 4 ] ;

• For the { w = 68 } cell , marked-off in { dark-grey color } above , we have :
  • [ 68 ] = 22 * [ 3 ] + [ 2 ] ,
  • [ 68 ] = 13 * [ 5 ] + [ 3 ] ,
  • [ 68 ] = 9 * [ 7 ] + [ 5 ] .

Let us now make this rather interesting observation :

• when we move from the { w = 66 } cell to the { w = 67 } cell ,
  • we move in the general diagonal ( 1 , 1 , 1 ) direction ;

• when we move from the { w = 67 } cell to the { w = 68 } cell ,
  • we also move in the general diagonal ( 1 , 1 , 1 ) direction .

Let us now take a closer look at this phenomenon , by bringing-in 2 sets of { 3-layer diagrams } :

• for the set of { 3-layers diagrams } on-the-left , below :
  • we have marked-off , in { dark-grey color } , the cells for { w = 0 , 1 , 2 , 3 , 4 , 5 , 6 } ;

• for the set of { 3-layers diagrams } on-the-right , below :
  • we have marked-off , in { dark-grey color } , the cells for { w = 7 , 8 , 9 , 10 , 11 , 12 } .

Our proposal for the construction of this { 3 x 5 x 7 } Box , [ modulo 105 ] is then as follows :

• We start-off with a [ 0 ] for the cell closest to the { Point-Of-Origin } , { POINT O } .

• We then move in the ( 1, 1, 1 ) direction to the next cell and place a [ 1 ] there ;

• We then move in the ( 1, 1, 1 ) direction to the next cell and place a [ 2 ] there ;

• We keep on moving in the ( 1, 1, 1 ) direction to place the next [ number ] , but :
  • whenever we 'hit' a wall , we go-thru-the-wall and come-back-thru-the-opposite-wall to the next cell ,
    • as we have done in the left-hand-side set of 3 diagrams , above , when we move from [ 2 ] to [ 3 ] .

• We finally end-up at [ 104 ] , where the three (3) outer-walls meets .

In certain sense , this is akin to a { division by geometric construction } !?

We simply note here that the equation :

• [ W ] = 70 * X + 21 * Y + 15 * Z

can also be writtten in this format :

[ W ] is then the [ DOT Product ] of the two (2) vectors :

• [ 70 , 21 , 15 ] , &
• [ X , Y , Z ] .

And we bring-in this final diagram for further thoughts :