Structure of the Multiplication Table for [ modulo P ]

In this Section, we shall find out why { FIRON - 2/P } is controlling on the size of the { RING's } .

And we also recognize { FIRON - 2/P } as the 2nd-most important property for [ modulo P ] , [ P ] being a { prime number } ,

• with the value [ Q ] = [ P - 1 ] , arising from the { Fermat Little Theorem } , taking 1st place .

For the 'odd' { prime number } , [ P ] , greater than [ 3 ] , we again set-up the value [ Q ] such that :

• [ Q ] = [ P - 1 ]

We then define { FIRON - 2/P } as the smallest non-zero value of [ N ] satisfying the equation :

{ FIRON } then stands for the { FIRst instance of ONe } , and that is to say :

• In the search for the value of { FIRON - 2/P } , we always go thru the processs of :
  • successively evaluating the value for the expression ,
    • 

    always starting-off with the value of [ N ] being equal to [ 1 ] , i.e. :

    • 

  As we increase the value of [ N ] , the value of the { expression } also changes accordingly ,

  • and we take the value of [ N ] as being [ FIRON - 2/P ] , at the first instance of :
    • 

    and this situation is known as the { First-Instance-Of-ONE } .

We then have these two (2) equations below as being always true & valid :

• 

• , for all non-zero values of [ N ] less than [ FIRON - 2/P ] ;

  by the definition of { FIRON - 2/P } above .

We also define , in general , { FIRON - Y/P } as the smallest non-zero value of [ N ] satisfying the equation :

• ,

  with the range of [ Y ] being the full range from [ 1 ] to [ Q ] .

We note here , first-of-all , that { FIRON - 1/P } is always equal to [ 1 ] , arising from :

For all values of [ Y ] in the range of [ 2 ] to [ Q ] , we can again go thru the search process of :

• successively evaluating the value for the expression ,
  • 

  always starting-off with the value of [ N ] being equal to [ 1 ] , i.e. :

  • 

  And as we increase the value of [ N ] , the value of the { expression } also changes accordingly ,

  • and we take the value of [ N ] as being [ FIRON - Y/P ] , at the first instance of :
    • 

    and this situation is , again , known as the { First-Instance-Of-ONE } .

Then , for the value [ Y ] in the range of [ 2 ] to [ Q ] , we always have these two (2) equations below as being true & valid :

• 

• , for all non-zero values of [ N ] less than [ FIRON - Y/P ] ;

  by the definition of { FIRON - Y/P } above .

Let us now take note of a very special property of { FIRON - Y/P } , namely :

• If we were able to identify a non-zero value of [ E ] satisfying the equation :
  • 

  then :

  • [ FIRON - Y/P ] is always divisible into [ E ] .

For the case of [ Y ] being equal to [ 1 ] , this is trivial :

• because [ FIRON - 1/P ] is always equal to [ 1 ] , and [ 1 ] is always divisible into [ E ] .

For the case of [ Y ] being in the range of [ 2 ] to [ Q ] :

• We first establish that :
  • the value of { FIRON - Y/P } is always smaller than or equal to the value of [ E ] .

    This is because :

    • while the value [ E ] , in itself , marks an { Instance-Of-ONE } , i.e. :
      • 

      { FIRON - Y/P } always marks the { First-Instance-Of-ONE } , i.e. :

      • 

      • , for all non-zero values of [ N ] less than [ FIRON - Y/P ] ;

      so that :

      • the value of [ E ] cannot possibly be smaller than the value of { FIRON - Y/P } .

• And { consistancy } between the two (2) key equations , i.e. :
  • 

  • 

    can only be maintained if and only if :

    • [ FIRON - Y/P ] is divisible into [ E ] .

  This is because , if otherwise , contradictions must result .

  And let us take a quick look here into just what these contradictions might be :

  • Let us assume , for-the-time-being , that :
    • { FIRON - Y/P } is not divisible into [ E ] ,

    so that we may express [ E ] in the following manner :

    • [ E ] = [ n ] * [ FIRON - Y/P ] + [ R ]

      where :

      • [ n ] is the 'quotient' & [ R ] is the 'remainder' ,

        with the overriding condition on [ R ] being :

        • 0 < [ R ] < [ FIRON - Y/P ] .

    Let us now bring back the 1st key equation from above :

    • 

    Substituting the value of [ E ] therein , then bring us to this equation below :

    • 

    and on expansion , we have :

    • 

    But we have already established that :

    • 

    This then necessarily lead us to conclude that :

    • 

      which is contradictory to the fact the { FIRON - Y/P } is the { First-Instance-Of-ONE } ,

      • because [ R ] is smaller than [ FIRON - Y/P ] !

Thus , we can conclude that { FIRON - Y/P } is necessarily divisible into [ E ] .

Let us now take a look at the relation between [ FIRON - 2/P ] and the value [ Q ] ,

• in-light-of this last conclusion we have in { Topic #5 } immediately above .

For this purpose , let us now bring-in the { Fermat Little Theorem } , which states that :

• , for any { prime number } [ P ] .

We then have this derived equation , for the value of [ Z ] being equal to [ 2 ] :

• , [ Q ] being equal to [ P - 1 ] , as always .

We then bring back this 'defining' equation for { FIRON - 2/P } , from { Topic #3 } above :

And these two (2) equations together then tell us that :

• [ FIRON - 2/P ] is always divisible into [ Q ] ,

  based on our findings / conclusion in { Topic #5 } immediately above.

Let us now express this relation via this equation below :

• [ Q ] = [ T ] * [ FIRON - 2/P ] ,
  • where [ T ] is a { positive integer } .

We then have this table for the values of [ FIRON - 2/P ] , [ T ] , & [ Q ] :

• for all { 'odd' prime numbers } less than [ 256 ] ,

  for the reader's first perusal & familiarization with the variation / variety inherent in { FIRON - 2/P } .

And we shall find out why { FIRON - 2/P } is controlling on the 'Square-Of-Square' { RING's } , next .

Let us now demonstrate why { FIRON - 2/P } is controlling on the 'Square-Of-Square' { RING's } .

• by bringing back the { RING OF 28 } for the { prime number } [ 233 ] , i.e. :
  • [ 233 ] = 8 x 29 + 1

• And each of the 28 { numbers } on this { RING OF 28 } then satisfies the equation :
  • 

Let us now arbitrarily pick any one of the { 28 numbers } on the { RING OF 28 } for our demonstration here :

• and we shall pick the number [ 23 ] , for this-time-round .

Let us now do a { keep-on-squaring } process on the number [ 23 ] , to find out :

• if we do arrive back at [ 23 mod 233 ] at some later stage ;

• and if so , how many { 'squaring' operations } does it take .

And we were able to establish that it takes 28 { 'squaring' operations } to arrive back at [ 23 mod 233 ] ,

• as per the set of { 28 equations } to-the-right of the diagram , above .

We can then write , for the 28 { 'squaring' operations } :

or ,

Let us now bring-in the more general format for this equation , i.e. :

And we see here that the value of [ N ] is controlling on the size of the 'Square-Of-Square' { RING } , and in particular :

• the smallest non-zero value of [ N ] satisfying this equation here then determines :
  • the minimum number of { 'squaring' operations } required to arrive back at the same { number } [ modulo P ] ,

  • and therefore the size of the 'Square-Of-Square' { RING } itself .

But before we can make-a-move on the above equation ,

• let us first take a closer look at this overriding equation for the value [ Y ] , [ Y ] being a { number } on the ' Square-Of-Square' { RING } :
  • ,

    with :

    • [ F ] being an { 'odd' prime factor } of [ Q ] ,

    • [ Y ] being a [ solution value ] to the equation , other than the universal solution [ 1 ] , i.e. :
      • [ Y ] is not equal to [ 1 ] ,

        because [ 1 ] is always on the { Characteristic Pyramid } & never on a { RING } .

We shall now make a key observation here :

• [ F ] is the value [ FIRON - Y/P ] .

  This is because :

  • the equation above , i.e. :
    • 

    in-itself-and-by-itself , dictates two (2) things :

    • { FIRON - Y/P } cannot exceed the value [ F ] , i.e. :
      • { FIRON - Y/P } is either smaller or equal to the value [ F ] ;

    • { FIRON - Y/P } is always divisible into the value [ F ] ,
      • whether { FIRON - Y/P } is itself smaller , or alternately equal to , the value [ F ] .

  • But [ F ] is a { prime number } and the only factors divisible into [ F ] are [ 1 ] & [ F ] ;
    • and [ 1 ] is ruled-out as a choice because [ Y ] is not equal [ 1 ] ,

      and this 'forces' us to conclude that [ F ] is indeed the value [ FIRON - Y/P ] .

We are now ready take a closer look at the equation :

Let us now 'divide' both sides by [ Y mod P ] to arrive at this equation below :

Let us recall that we have established that [ F ] is indeed the value [ FIRON - Y/P ] , and we can now bring-in these 2 'governing' equations , as follows :

• 

• , for all non-zero values of [ N ] less than [ F ] .

We can then conclude that [ F ] is necessarily divisible into [ 2^N - 1 ] ,

• in order that { consistancy } be maintained among the 3 equations immediately above .

Thus , we can now write :

yielding :

And the smallest non-zero value of [ N ] satisfying this equation is then the value [ FIRON - 2/F ] .

Thus , { FIRON - 2/F } is controlling on the 'Square-Of-Square' { RING's } arising from :

And we shall be taking a quick look at 2 examples , next , for a better understanding / appreciation of this very special feature .

Let us now take a look at the { Mersenne Prime } [ 2,147,483,647 ] ,

• being equal to [ 2^31 - 1 ] .

And we can write :

• 2,147,483,647 = 2 x 3 x 3 x 7 x 11 x 31 x 151 x 331 + 1

And let us write-down what we would expect on the 'Square-Of-Square' { RING's } for [ modulo 2,147,483,647 ] ,

• based on our discussion in the last { Topic } above , as follow :

  Prime [ P ]	FIRON - 2 / P	Value of T	Value of Q		Expectation on 'Square-Of-Square' { RING's }
  3	2	1	2		1 x { RING OF 2 }
  7	3	2	6		2 x { RING's OF 3 }
  11	10	1	10		1 x { RING OF 10 }
  31	5	6	30		6 x { RING's OF 5 }
  151	15	10	150		10 x { RING's OF 15 }
  331	30	11	330		11 x { RING's OF 30 }

And we can confirm that we do have 6 x { RING's OF 5 } for the solution to the equation :

• 

  other than the universal solution [ 1 ] ,

  as per this set of 6 diagrams to follow .

And we have marked-off 3 pairs { multiplicative conjugates } for [ modulo 2,147,483,647 ] here , for indicative purposes :

• the 1st pair is in { white-color } ,
• the 2nd pair is in { yellow-color } , &
• the 3rd pair is in { purple-color } ;

  in the set of 6 diagrams , above .

And we simply note here that the 2 members of each pair , in these 6 x [ RING's OF 5 ] , are always on separate { RING's } .

Let us now take a brief look at the { prime number } [ 173 ] , i.e. :

• [ 173 ] = 4 x 43 + 1

And we take special note here that :

• [ FIRON - 2/43 ] = 14 , so that :

  3 x { RING's OF 14 } are expected for [ modulo 173 ] .

We then have the { Characteristic Pyramid } & the 3 x { RING's OF 14 } for [ modulo 173 ] as follows :

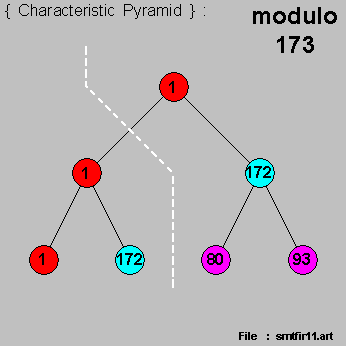
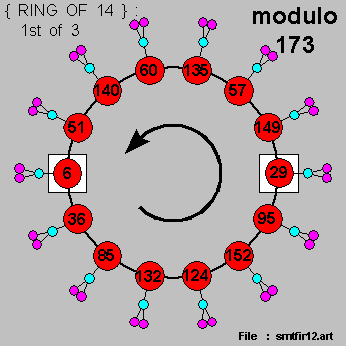
And we have marked-off 3 pairs of { multiplicative conjugates } for [ modulo 173 ] here , for indicative purposes :

• the 1st pair is in { white-color } ,
• the 2nd pair is in { yellow-color } , &
• the 3rd pair is in { purple-color } ;

  in the 3 diagrams for the { RING's OF 14 } , above .